Calcule , onde e é definida por:
Com campo de vetores normais exterior a .
Passo 1
Vamos fazer um desenho da imagem somente para entender melhor o problema!
Fica mais fácil de visualizar o que precisamos fazer!
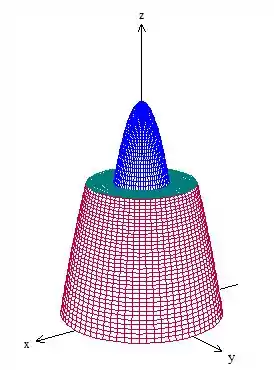
Passo 2
A superfície não inclui a base do sólido, o disco com a normal desta base apontando para fora do sólido, ou seja, na direção negativa do eixo . Logo, teremos,
Onde, é o sólido fechado, é a “tampa” do sólido e é a superfície original. Vamos começar calculando o divergente do campo:
Assim,
Passo 3
Desta forma, pelo Teorema de Gauss, temos:
Ou seja, para calcular o que pede o enunciado, basta calcular o fluxo que passa pela base. A base é o plano limitado pela circunferência .
Passo 4
Parametrizando a base, temos:
Como a normal de uma parametrização explícita é:
Para a orientação no sentido negativo de ,
Passo 5
Assim, podemos calcular o fluxo na base do sólido,
Para resolver esta integral, vamos usar as coordenadas polares,
Resposta
Assim, o fluxo