Questão 3:
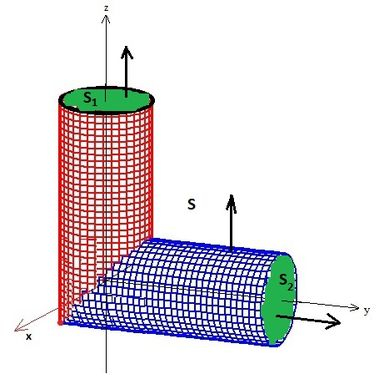
Seja a superfície regular por partes. , onde é o pedaço do cilindro de equação implícita acima do plano e abaixo do plano , e é o pedaço do cilindro de equação implícita abaixo do plano e com . Consideremos a orientação de tal que o campo de vetores normal unitário aponta para fora dos cilindros.
Seja o campo espacial
- Faça um esboço de (Dica: esboce o eixo apontado para a direita).
- Calcule o fluxo de através de (Dica: Feche com duas tampas e aplique o teorema de Gauss).
Passo 1
Parece uma superfície super chata para esboçar, neh? Mas quer uma dica, abstrai as informações primeiro. Olha só, sabemos que o cilindro de raio dois e centrado em ... , faz parte da superfície...
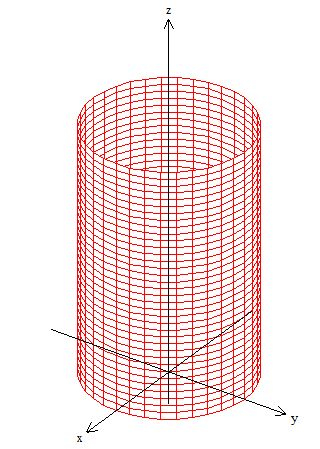
Outro cilindro que também faz parte de é o que também tem raio , porém esse está deitado ao redor de , ...
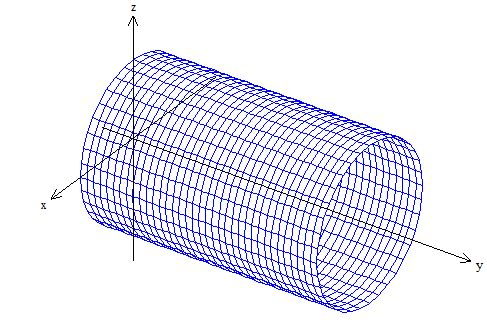
Repare que pelo fato desses dois cilindros terem o mesmo raio, ambos se intercedem um ao outro, como se um estivesse dentro do outro.
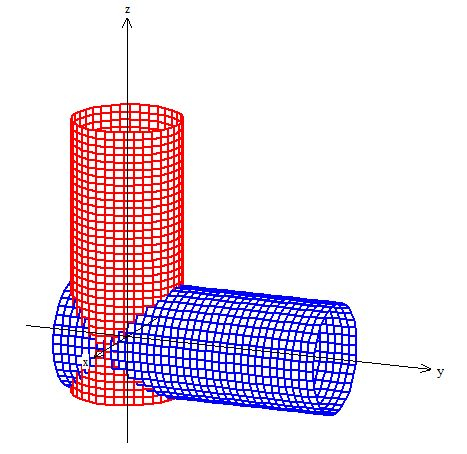
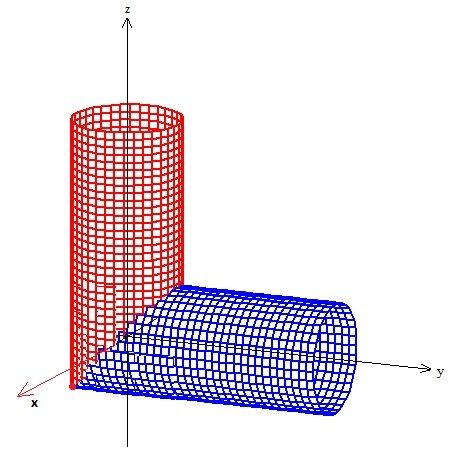
Agora, uma outra superfície que também entra na brincadeira é o ... Um plano paralelo ao eixo e que não por coincidência corta esses dois cilindros justamente nessa diagonal aqui oh:
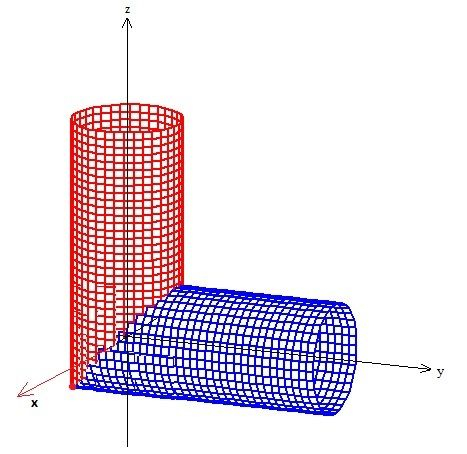
Eu disse que não por coincidência, afinal se fizermos a intercessão matemática dos dois cilindros, ou seja, resolver o sisteminha...
Sacou? No caso a superfície então é esta daí de cima, já que o cilindro de cima está acima desse plano, e o cilindro deitado abaixo, é...
Percebeu?
Passo 2
Bem, um fluxo de um campo vetorial por uma superfície é dado por uma integral de superfície. Assim...
Porém, calcular essa integral de linha como está aí vai ser muito complicado, pois o campo não é muito simpático com a gente. Por isso, a ideia é justamente seguir a dica e aplicar o teorema de Gauss.
Mas mesmo assim, para termos certeza de que estamos no caminho certo aplicando o Teorema de Gauss, sempre é aconselhável que calculemos o diverte primeiro. Então bora?
Passo 3
Como o campo...
Calculando essas derivadas parciais...
Com um divergente simples desses, sim! Vamos de fato aplicar Gauss... Após, é claro, que observarmos se estamos em suas condições .
Passo 4
De acordo com o teorema de Gauss, precisamos:
1º - Uma região delimitada por uma superfície fechada .
2º - Uma superfície orientada positivamente.
3º - Um campo sem singularidades.
Passo 5
Bem, o sólido que estamos trabalhando...
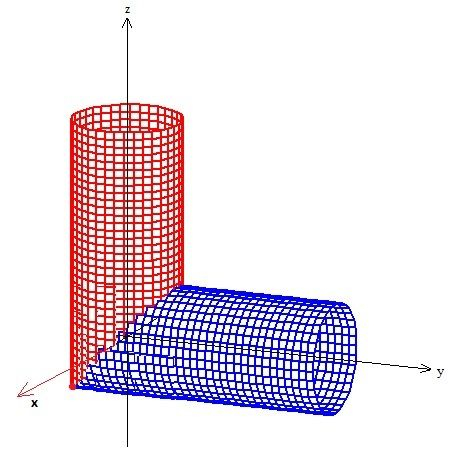
Não é fechado, mas de acordo com a dica, podemos fechar tampando esses dois buracos com duas superfícies circulares que chamaremos de e ...
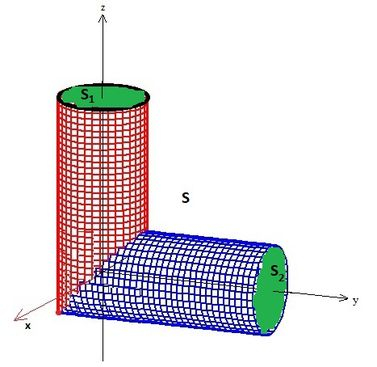
Assim, a borda da região fechada é .
Passo 6
Precisamos de superfícies orientadas positivamente, ou seja, com o vetor saindo do sólido . Isso já acontece lá do enunciado para a superfície ...
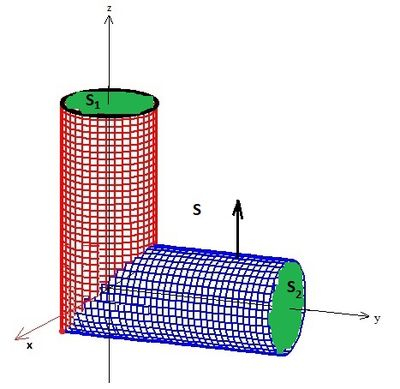
Para as superfícies que adicionamos, basta colocar...
Passo 7
Precisamos também de um campo sem singularidades onde estamos trabalhando. Se olharmos para o campo vetorial...
Como não temos nenhum problema de definição em nenhum ponto, como uma divisão por zero ou algo assim, o campo está ok.
Passo 8
Nas condições do Teorema, podemos aplicar a igualdade de Gauss:
Bem, como já vimos, a borda do sólido fechado é ...
Como queremos a integral de superfície em cima de (os cilindros), isolemos...
Se queremos a integral de superfície em cima , basta calcular essas três integrais e matar o problema (embora pareça que estamos ficando maluco por fazer três integrais ao invés de uma de superfície, ainda é o processo mais rápido, vai por mim ). Bora lá?
Passo 9
Vamos começar pela integral tripla...
Precisamos descrever o sólido para substituir aí. Como temos dois cilindros, vamos ter que separar essa integral tripla em duas...
Onde o representa o cilindro acima do plano enquanto que o o cilindro deitado abaixo de , saca?
Passo 10
Para a primeira integral, em cima de , como estamos usando um cilindro, podemos usar as coordenadas cilíndricas...
Onde o , varia ao redor do eixo , portanto ele deve dar uma volta completa...
Enquanto o , ele deve variar de até o raio máximo que é o raio do cilindro vermelho...
Já o , bem, ele está saindo do plano e indo até o limite máximo que é ...
Assim
Substituindo os limites de integração em ...
Como ...
Passo 11
Calculando a segunda integral tripla...
Primeiro precisamos mudar para coordenadas no caso cilíndricas também, só que...
também dá uma volta completa ao redor do aqui...
O ...
Enquanto que o varia de ao ...
Montando a integral tripla...
Hey, é a mesma integral, a única diferença era no nome da variável de dentro. Isso não interfere no resultado, então...
E como a integral...
Sacou?
Passo 12
Agora calculemos a integral de superfície em cima de ...
Bem, parametrizando , por estar em cima de um plano ...
Onde os limites de e estão dentro do cilindro de equação .
Como o vetor normal unitário desse plano é...
Pois ele está pra cima, a integral de superfície fica...
Como a integral de é a área da superfície que nesse caso é um círculo de raio ...
Passo 13
Calculando a outra integral de superfície e não morra de tédio kkkkk
Nesse daqui, infelizmente não tem como de usarmos o que usamos não, pois o vetor unitário na direção de é e quando fizermos o produto com , não vai dar uma constante. Então teremos de fazer do jeito clássico, ou seja, primeiro parametrizar a superfície...
Como estamos em cima de um plano
Onde e variam dentro do cilindro .
Para encontrar ...
O vetor normal pode ser encontrado pelo Bizu, já que parametrizamos como gráfico de função...
Substituindo os termos no campo ...
Jogando essa três coisas na integral de superfície...
Usando coordenadas polares...
onde varia de a 2 e de até .
Passo 14
Voltando então para a integral que queremos...
Resposta