15) Considere o campo vetorial , seja a calota esférica , com e raio . Sabendo que o fluxo de na direção da normal exterior é igual a , calcule o raio da calota.
Passo 1
Bem, vamos com calma aqui. Um fluxo nada mais é do que uma integral de superfície...
Em cima de que nos representa uma “calota” de um raio :
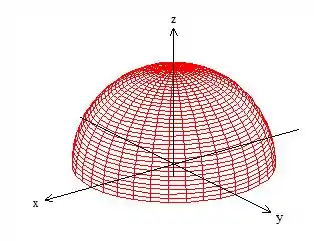
Podemos resolver uma integral de superfície dessa de formas basicamente:
1º - De uma forma direta.
2º - Ou... Utilizando o Teorema de Gauss.
Normalmente o Teorema de Gauss é mais fácil e mais rápido, mas a princípio não temos como garantir que método é mais fácil. Mas uma boa dica de qual caminho tomar é sempre calculando o divergente:
Como
Calculando as derivadas parciais:
Logo...
Pow, com um divergente desses... Sim, o problema está pedindo que façamos por Gauss!
Passo 2
O teorema basicamente é a igualdade maravilhosa:
Mas não podemos aplicar essa integral assim... De qualquer forma. Precisamos averiguar as condições do Teorema que nos pede:
1º - Uma superfície fechada delimitando o sólido .
2º - Sem singularidades na função Vetorial.
3º - Superfície orientada positivamente.
Vamos passar por cada um deles e verificar se satisfazem ou não 😊!
Passo 3
Quanto ao primeiro quesito, ter uma superfície fechada, já falhamos nesse primeiro requisito. Afinal de contas a nossa calota é uma superfície aberta:

Veja que a calota é apenas a parte de cima da esfera cortado pelo pano . No caso, temos a liberdade pelo teorema de Gauss de fechar essa superfície o que no caso vamos fazer justamente com o plano ...
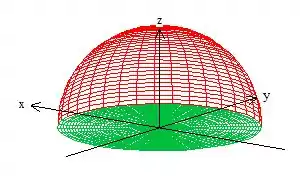
A essa superfície que acabamos de adicionar, daremos um nome de , mas não se preocupe, é apenas um nome ok?
Passo 4
Quanto ao segundo e ao terceiro quesitos...
2º - Sem singularidades na função Vetorial:
Esse campo Vetorial funciona em todas as situações, afinal ele não tem nenhuma divisão por ou algo do tipo.
3º - Superfície orientada positivamente:
Bem, isso significa que precisamos de uma superfície com vetores normais saindo do sólido fechado por ela, o que já acontece lá do enunciado:
“ na direção da normal exterior ”
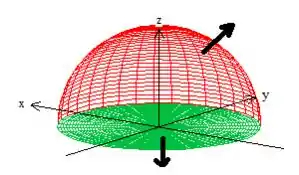
Passo 5
Bem, com as três condições sendo satisfeitas, podemos aplicar a igualdade do Teorema sem nenhuma restrição...
Aqui só tenho um detalhe que preciso te falar! A integral de superfície do teorema é calculada em cima da superfície que fecha o sólido . E esse cara é
Logo, temos que desmembrar a integral de superfície em duas...
Então se queremos a integral de superfície, calculemos a integral tripla e essa outra integral de superfície que cara, vai dar muito menos trabalho, acredita em mim!
Vamos só fazer mais simplificações aqui... Passando a integral de pro outro lado...
Veja que podemos mudar o sinal dessa integral de superfície em ...
Caso ao invés de pegar o vetor normal pra baixo como vimos no passo anterior, pegarmos o outro... O virado pra cima...
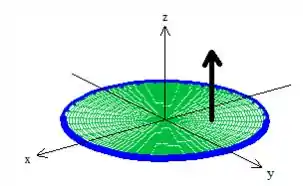
Passo 6
Começando pela integral tripla...
Bem, quem é a integral de um ? Sim! Você já sabe que é o volume de um sólido...
Como é a metade de uma esfera de raio ...
Passo 7
Bem, ainda não acabamos o problema, pois precisamos de eliminar a integral de superfície em ...
E essa, infelizmente não temos truques. Precisamos calcular na marra:
1º - Parametrizar a superfície .
2º - Calcular .
3º - Trocar os termos do campo pelos termos da parametrização.
Passo 8
Precisamos da superfície parametrizado para prosseguir com os cálculos:
Como é um círculo, podemos parametrizar utilizando coordenadas cilíndricas...
O do círculo é conhecido (ele está em cima do plano )...
Então a gente pode em uma notação mais elegante, falar que a parametrização é...
Onde e varia com o círculo. podemos afirmar de antemão que ele dá uma volta completa, logo...
Já o raio, depende do raio do círculo. Bem, podemos encontra esse raio fazendo o na equação da esfera...
Ou seja, é um círculo de raio , logo, o raio varia de até esse cara, veja...
Passo 9
O termo dessa parametrização é...
Onde
Logo...
Veja que esse é exatamente o vetor normal de que precisamos, ou seja, apontando pra cima 😉
Passo 10
Voltando para a integral que precisamos resolver...
Substituindo os caras...
Agora trocando o pelas variações de e e tirando esse daí e colocando sua correspondente que vimos na parametrização ...
Passo 11
Veja bem, encontramos o valor da integral em . Mas como vimos do teorema de Gauss...
Então
Como a integral de superfície em pelo enunciado valia...
Então...
Como , então o raio só pode ser...