Questão 3: Seja a região do exercício . Seja a parte da fronteira que contem o pedaço de paraboloide de cilindro. Calcule o fluxo
Do campo espacial , onde está orientada positivamente (como parte da fronteira de ). Dica: Aplique o teorema de Gauss a ).
Passo 1
Bem, de acordo com o exercício , temos uma região definida desse jeito aqui:
E cujo desenho é esse:
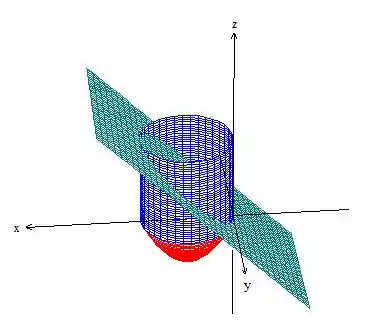
Ora, se queremos a integral de superfície em (parte do paraboloide com o cilindro) podemos usar o Teorema de Gauss pra isso mesmo, já que o Teorema de Gauss nos fala o seguinte:
Agora, para aplicar essa igualdade, temos que estar dentro de algumas hipóteses:
- Temos que ter uma superfície fechada borda de .
- Precisamos de uma orientação positiva.
- O campo não pode ter nenhuma singularidade.
Vamos verificar cada hipótese e em seguida calcular a integral de superfície através de Gauss !
Passo 2
Bem, infelizmente a superfície que estamos trabalhando não é à borda da região , mas é quase (é a superfície ):
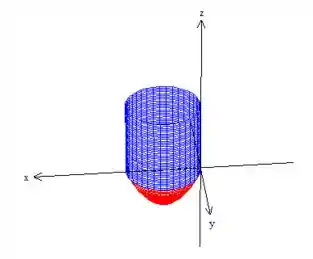
Então, como se trata de uma superfície aberta, podemos fecha-la com o próprio plano formando a borda de : .
Ora, como a borda é a composição tanto da superfície quanto do plano que vamos chamar de :
Passo 3
Precisamos de uma orientação positiva na superfície , isso significa que o campo de vetores normais deve estar saindo da superfície , o que já acontece por definição
Passo 4
Com relação ao último quesito:
Devemos verificar se o campo tem ou não singularidades onde estamos trabalhando:
Por sorte tal campo não tem nenhum problema de definição!
Passo 5
Finalmente, após verificar tudo, podemos de fato aplicar a igualdade do teorema de Gauss para resolver o problema:
Contudo, como
Então se queremos encontrar a integral em , basta calcular essas outras duas integrais e matar o problema por Gauss !
Passo 6
Primeiro calculemos a integral tripla:
Como o é:
Onde...
Derivando...
Então...
Passo 7
Ora, para calcularmos essa integral tripla, como estamos no interior de um cilindro deslocado:
Acho interessante se mudarmos para as coordenadas cilíndricas deslocadas:
E uma equação útil é a equação do cilindro deslocado somando esses e ao quadrado...
Agora, precisamos saber onde essas variáveis giram no interior do nosso sólido:
Perceba que o raio varia de (eixo do cilindro deslocado) ao raio máximo :
dá uma volta completa:
Enquanto o varia da base formada pelo paraboloide até o teto com o plano
Nas novas coordenadas...
Assim:
Calculando a integral de dentro...
Integrando a do meio agora...
Por fim...
Passo 8
Calma jovem gafanhoto! Ainda falta mais uma integral:
Para calcular essa integral de superfície e matar o nosso, devemos:
- Parametrizar a superfície.
- Calcular o termo
- Mudar os termos de para os termos da parametrização.
Vamos nessa?
Passo 9
Poxa, estamos lidando com um plano , então nada mais justo que parametrizarmos utilizando parametrização explícita, onde podemos encontrar todos os pontos do plano assim:
Onde e variam dentro do cilindro:
Passo 10
Para calcular o termo , podemos fazer:
Onde
Agora, perceba que esse vetor normal aí está apontado pra cima e o que queremos tem que estar exatamente pra cima. Logo:
Passo 11
Por último, antes de retornarmos à integral, devemos trocar os termos da parametrização no campo :
Passo 12
Então...
Ora, a integral dupla de é a área da região . Como se trata de uma área circular de raio ...
Passo 13
Como vimos...