Calcule , onde e é definida por e
Passo 1
Esse problema ai parece ter uma superfície muito complexa, né? Dá pra imaginar que não vamos fazer essa integral de superfície da maneira convencional, vamos ter que usar algum teorema. Nesse caso aqui o mais apropriado é o Teorema de Gauss, o enunciado dele é esse aqui:
Onde é a fronteira do sólido . Para aplicarmos isso no nosso problema, precisamos de uma superfície fechada! O enunciado descreve a superfície S em três outras, vamos ver como ficam juntas? O esboço é assim:
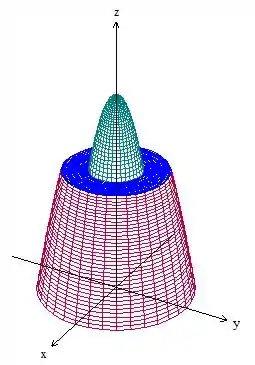
Só pra confirmar que as interseções das superfícies de fato são iguais, tenta ver os valores máximos e mínimos de cada uma das três superfícies, assim:
A primeira superfície descrita, a vermelha, foi
Em ela é a circunferência
Em ela é a circunferência
A segunda superfície descrita, a azul, foi
Que está no mesmo ponto que a primeira acaba e vai da circunferência de raio até o raio igual a
A última superfície descrita começa em e no resto é fechada! Portanto viu que tudo se completa, né? Só tem um problema, essa superfície não tem uma base, ela é aberta no plano
Para usar o teorema de Gauss vamos ter que acrescentar uma superfície
Dessa forma,
Nos próximos passos vamos calcular esse divergente e a integral dessa superfície pra chegar no resultado final, vamos lá?
Passo 2
Vamos começar pelo divergente de , vamos calculá-lo pela fórmula
Nosso campo é esse aqui
Ótimo! Se o divergente é igual a zero, não precisamos fazer a integral tripla! Podemos dizer que
Passo 3
Vamos para a nossa integral da superfície , a primeira coisa a se fazer é encontrar a sua parametrização. Ela é um círculo de raio 3 no plano , certo? Então podemos parametrizar assim:
Antes de substituir tudo ne forma desnecessária no campo , vamos ver como fica a normal dessa superfície, onde ela for zero não vamos precisar nem olhar pro campo!
A normal é dada pelo seguinte produto vetorial
Mas, para usarmos o teorema de Gauss, as normais das superfícies devem estar voltadas para fora do sólido! Essa aqui, graficamente está pra dentro, o que não é um problema, só invertermos os sinais
Muito bom, dois termos zeraram! Precisamos só pensar no terceiro termo do campo , ele é o seguinte
Passo 4
Vamos juntar o campo e a normal na integral de superfície de
Antes de integrar isso ai vamos usar essa relação aqui
Voltando pra integral
Passo 5
Voltando para o teorema de Gauss