Encontre o fluxo do campo através da superfície , orientada positivamente, , onde , e , .
Passo 1
Vamos começar entendendo essas duas superfícies e , repara que vamos ter uma figura mais ou menos assim
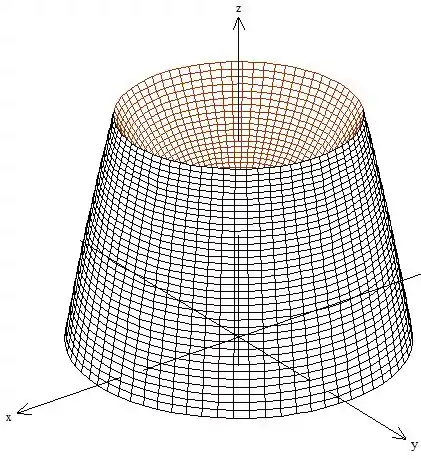
Ele quer o fluxo dessa parada, ou seja, a integral dupla ao longo do campo , é interessante tentar aplicar teorema de Gauss aqui, isso porque essa função é meio complicada e se fizermos uma conta rapidinha do divergente vamos ver que ele é . O problema é que precisamos fechar essa superfície com que seria aquela elipse de quando
Vamos achar o divergente dessa função
Então tudo se resume a achar o fluxo ao longo de que é bem mais fácil de resolver, vamos ver como ficar essa bagunça antes de qualquer coisa
Então tudo se resume a achar a integral de superfície ao longo de .
Passo 2
Vamos entender essa superfície, repara que ele quer tudo orientado positivamente, ou seja é para fora desse solido que montamos, repara que está no plano isso nos diz que, orientando o vetor para fora, o vetor normal vai ser
A integral de superfície vai ficar
Vale a pena lembrar também que em , então a integral fica
A área da elipse vai ser
Onde e são os eixos da elipse, lembra da equação dela?
Então os eixos vão ser e , e a área vai ficar
Isso nos diz que
Passo 3
A integral de superfície vai ser
Substituindo o valor que achamos