Calcule , onde e é a superfície definida por:
Com o campo de vetores normais exterior a .
Passo 1
Antes de tudo, vamos fazer um esboço dessas superfícies. Temos um paraboloide virado para baixo cortado em e , um anel em e outro paraboloide :
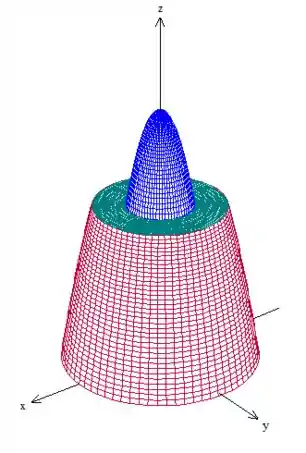
Repara que todas essas superfícies encaixam bonitinho (pode conferir nas equações delas). Onde termina uma começa a outra.
Foi?
Passo 2
Como o campo tem uma expressão meio complicada, nem rola calcular isso aí pela definição. Vamos tentar usar Gauss, ok?
Vamos começr calculando o divergente disso aí:
Gente, deu zero, que lindo.
Passo 3
Show, agora vamos aplicar o teorema. Para isso, vamos fechar essa região com esse círculo em , ok?
Onde é a região limitada por e as normais às superfícies apontam para fora.
Passo 4
Agora, precisamos da integral na disco. Repare que quando o paraboloide encontra o plano :
Temos uma circunferência de raio . Logo, nosso disco tem esse raio. Vamos parametrizá-lo em coordenadas polares:
Onde e .
Passo 5
Agora vamos encontrar a normal a essa superfície:
Bem, se as normais devem apontar para fora, quer dizer que, no plano, a normal é para baixo. Portanto, queremos o vetor oposto a esse:
Passo 6
Certo, agora vamos usar essa fórmula aqui:
Agora é só resolver
Passo 7
Temos então