Seja a parte do hiperboloide , com , orientada de modo que a normal unitária satisfaça . Então

é igual a:

a)

b)

c)

d)

e)

Cara, Gauss tem umas condições para aplicar. Uma delas já atendemos:

- nosso campo está bem definido em todo (já que não temos nenhuma restrição no domínio, tipo um denominador que pode zerar).

Maaas, não atendemos duas delas. Como assim? Os vetores normais precisam apontar para a parte externa de uma superfície fechada.

- Temos um hiperboloide de uma folha (porque só tem um termo negativo). Ele é aquela superfície que parece um tronco de árvore. Isso significa que a nossa superfície não está fechada em cima e embaixo.

O que a gente faz? Chora? Não! A gente vai fechar esse cara. Com planos em formato circular, porque planos são simples. Aí a nossa superfície geral vai ser o hiperboloide mais dois planos circulares.

Repara nesse gráfico lindão, lembrando que para o hiperboloide :

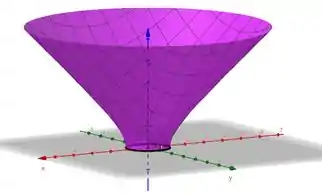
Podemos parametrizar o plano de baixo como:

A componente dele em é nula porque ele está em no espaço.

Repara que o nosso plano, para fechar a essa superfície por baixo, precisa ter o formato da interseção do hiperboloide com o plano , certo? A equação dela é:

Ou seja, uma circunferência. Nosso plano vai estar dentro dessa circunferência. Então a gente pode dizer que o domínio dele é:

Fazendo um raciocínio parecido para o plano circular que fecha nossa região por cima em , vamos ter:

Agora vamos montar nossa equação pelo teorema de Gauss. Ele diz que:

Esse é uma superfície fechada. No nosso caso, a superfície fechada é a soma de três superfícies. A semiesfera e os planos. Então a gente pode reescrever essa parte assim:

Lembra que nosso divergente deu 0:

Mas repara ele fala que a normal unitária ao hiperboloide satisfaz . Isso significa que a componente do vetor normal a ele está virada para cima.

Mas olha a figura dele de novo. Se o vetor normal dele está virado para cima sempre, significa que ele está virado para a parte dentro da superfície e não de fora, como o teorema de Gauss pede.

Isso significa que gente vai inverter o sinal da integral de para encaixar direitinho no teorema, como se estivéssemos multiplicando o vetor da superfície por para mudar de sentido. Então a gente tem:

Vamos calcular essas duas integrais da direita, aí achamos a que o enunciado pede.

O campo é aquele estranho né:

A nossa parametrização dos planos é:

A gente precisa começar achando o vetor normal a cada um desses planos. Mas repara que está dentro de e é também paralelo a esse plano.. O vetor normal a todo o é o vetor , que é o sentido do eixo , certo?

Então esse vai ser o nosso vetor para os dois planos? Cara, ele com certeza é normal as nossas superfícies, mas ele está apontando para fora da nossa região fechada em forma de tronco para os dois planos?

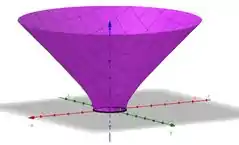
Em , ele está apontando para dentro da nossa região Para apontar para fora, ele precisa estar apontando no sentido oposto. Então só vamos multiplicar ele por :

Aí o nosso integrando para primeiro plano fica:

A gente precisa substituir as componentes do plano aí. E colocar o domínio da parametrização desse plano como o domínio da integral:

Agora repara que para o plano que está em , se o vetor aponta para cima, ele aponta para fora da região. Então a gente pode dizer que para ele:

Aí o nosso integrando para esse fica:

A gente precisa substituir as componentes do plano aí. E colocar o domínio da parametrização desse plano como o domínio da integral:

Voltando para o teorema, a gente tem:

Vamos usar as coordenadas polares para calcular essas duas integrais:

Para a primeira, temos um círculo completo de raio 1, então:

Para a segunda, temos um círculo completo de raio , então:

Aí nossas integrais mudadas ficam (não esquecendo do jacobiano):

Se a gente usar uma substituição simples nas duas derivadas, achamos que:

Calculando a integral de fora, achamos que: