Questão 3: Seja
Calcule
Onde é a superfície orientado pela normal unitária tal que
Passo 1
Poderíamos pensar em resolver essa integral de superfície de uma forma direta. Porém, esse campo não parece muito fácil de trabalhar. Então podemos pensar em uma saída muito bacana chamada Teorema de Gauss:
Mas assim, não podemos sair aplicando essa igualdade do nada. Temos que antes, averiguar as condições do teorema que nos exige:
- Um sólido delimitado por uma superfície fechada .
- Um campo sem singularidades.
- Uma orientação positiva.
Bora averiguar essas condições então?
Passo 2
Beleza, então veja que o problema quer que a gente calcule a integral de superfície em cima de ...
“Onde é a superfície .”
Se desenharmos essa superfície que é um paraboloide passando por quando passamos pelo eixo () e acima do plano :
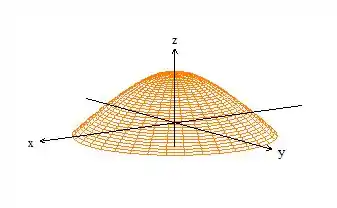
Veja que a nossa superfície é um cara aberto:
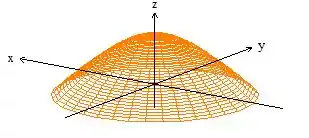
Então pelo teorema de Gauss, não poderíamos aplicar a igualdade, já que não temos uma superfície fechada. Porém, se considerarmos o disquinho no plano como superfície :
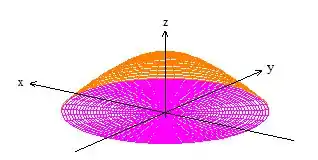
A junção da superfície com , gera essa superfície fechada que precisamos:
Então o teorema de Gauss fica...
Queremos a integral em , logo...
Passo 3
A segunda condição do teorema nos exige um campo sem singularidades onde estamos trabalhando:
O que acontece aqui já que para nenhum valor de , e esse campo dá problema.
Passo 4
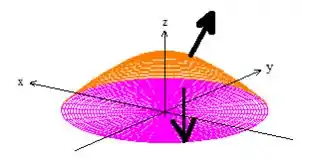
A última condição nos exige uma orientação positiva, o que significa que precisamos de vetores normais saindo do sólido:
E isso já acontece pelo próprio enunciado:
“... orientado pela normal unitária tal que ”
Já que significa o vetor normal apontado para cima na superfície (a vermelha), entende?
Passo 5
Com essas condições sendo satisfeitas, podemos voltar para o teorema...
Calcular cada uma dessas integrais do segundo membro, e matar o problema indiretamente pelo teorema de Gauss.
Eu sei... Parece que estamos ficando maluco, não é mesmo? Trocando a solução de uma integral por outras duas! Mas não se engane! Fazer isso, por incrível que pareça, é a forma mais fácil.
Passo 6
Vamos começar pela integral tripla
Calculando o divergente do campo...
Lembrando que , e são coordenadas do campo...
Calculando essas derivadas parciais...
A derivada em relação à de vai dar resultado análogo...
Enquanto isso...
Logo...
Passo 7
Então queremos uma integral assim:
Como estamos trabalhando dentro de um sólido de um paraboloide, podemos pensar em mudarmos as coordenadas para as cilíndricas:
O Jacobiano dessa mudança...
Além disso...
As variáveis dessa mudança “variam” dentro do nosso sólido:
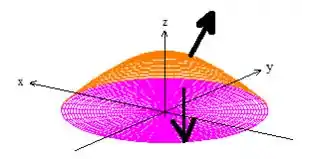
Veja que a variável vai de até o paraboloide:
Enquanto , varia de até o raio máximo que está definido pelo disco de intersecção do paraboloide com o chão ...
Logo...
Já o dá uma volta de ao redor do eixo para formar o sólido...
Sendo assim, a gente pode trocar os termos na integral:
Vamos integrar?
Passo 8
Começando pela integral de dentro...
Fazendo uma mudança então...
Mudando também os limites de integração...
Passo 9
Calma!!! Ainda não acabamos! Vamos agora calcular a integral de superfície:
Lembre-se que é o disco rosa que adicionamos para tampar o sólido:
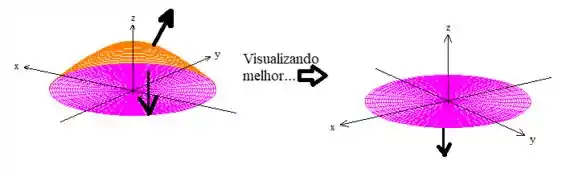
Esse disquinho sabemos que ele tem raio .
Uma coisa interessante, é que sabemos quem é esse vetorzinho normal aí pra baixo:
Então...
EPA! Integral de é a área da região (o disquinho de raio )
Passo 10
Voltando então para a integral de superfície que realmente queríamos láaaaa do passo ...
E substituindo cada um dos valores encontrados...