Seja a parte do paraboloide com , orientada pela normal unitária tal que e um campo vetorial de classe , definido em um aberto que contenha . Considere as afirmações:
(I)
(II)
(III)
Nessas condições, podemos afirmar que:
a) nenhuma das afirmações é verdadeira para todo campo .
b) apenas as afirmações (I) e (II) são verdadeiras para todo campo .
c) apenas as afirmações (II) e (III) são verdadeiras para todo campo .
d) apenas a afirmação (III) é verdadeira para todo campo .
e) todas as afirmações são verdadeiras para todo campo .
Passo 1
Vamos entender primeiro o que o enunciado quer nos dizer, beleza? Ele começa falando de , o paraboloide virado para baixo, mas cortado em e . Ele só existe entre esses dois valores. Olha num gráfico, ele só existe entre essas duas curvas azuis:
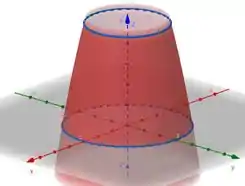
E ele diz que , isso quer dizer que o vetor normal a esse paraboloide aponta para cima (componente positiva). Já que a superfície está virada para baixo, esse vetor normal aponta pra fora da superfície.
Aí ele fala de , um campo bem definido no espaço onde está .
Agora que a gente tem a visão geral das coisas, vamos entrar nos itens. Vem comigo!
Passo 2
(I) Ele diz que
Cara, ele está relacionando uma integral tripla de um com uma integral de superfície. Quem pode fazer isso para gente? Aquele teorema que relaciona uma integral tripla, tendo um volume como domínio, com uma integral de superfície, o teorema de Gauss!
E o que esse bonito diz:
Sendo que deve ser uma superfície fechada e o espaço dentro dessa superfície.
Repara que na integral tripla desse item, esses extremos de integração descrevem o espaço dentro do paraboloide. Os extremos
Representam a parte de dentro de uma circunferência de raio , que é a projeção do paraboloide em . Mas repara que o extremo de diz isso:
Isso representa todo o espaço do eixo entre e o pico do paraboloide (que fica em ), mas o nosso paraboloide só vai até . Então ele nem está descrevendo nosso mesmo.
E lembra que nosso paraboloide é uma superfície aberta? A gente nem consegue usar Gauss nele assim diretão. Precisamos colocar dois planos aí no teorema para fecharmos nosso paraboloide em cima e embaixo.
Vemos que esse item viajou então, está tudo errado.
Passo 3
(II) Esse segundo item diz que
Ele está relacionando uma integral de superfície de um rotacional com uma integral de linha. Quem faz isso é o teorema de Stokes, e ele diz que:
Sendo que é uma superfície e é a fronteira dessa superfície. Quando a superfície tem mais de uma curva formando sua fronteira, como a nossa que tem duas curvas como fronteira, precisamos escrever uma soma de duas integrais de linha ali:
Mas repara que esse item só colocou uma integral de linha sobre uma curva no lado direito da equação. Ou seja, ele não está considerando que a nossa superfície tem duas curvas como fronteiras.
Repara aqui, as fronteiras da nossa superfície são essas curvas azuis que são circunferências mas de raios diferentes:
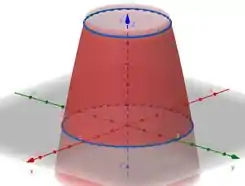
Então essa também está errada.
Passo 4
(III) Esse terceiro item diz que
É o mesmo caso do item anterior. Estamos usando teorema de Stokes. Será que aqui ele acerta o que errou no outro? Vamos ver!
De fato, agora a gente tem uma soma de duas integrais de linha do lado direito da equação, apontando para o fato de termos duas fronteiras. Mas será que essas integrais estão corretas?
Elas precisam descrever as fronteiras da nossa superfície, com uma orientação positiva. A gente percebe que de fato ele parametrizou essas curvas e substituiu isso na função do campo. Na primeira, ele parametriza a curva de cima:
Que está na altura e tem raio , porque se a gente fizer a interseção entre e :
Dá certinho uma circunferência de raio . Mas ela está orientada no sentido certo? De acordo com a parametrização, ela está no sentido anti-horário.
Para essa curva estar orientada positivamente, a gente tem que se imaginar andando nela, com nossos ombros e cabeça na direção e sentido do vetor normal a (esse preto, que a gente viu no começo que está orientado para fora).
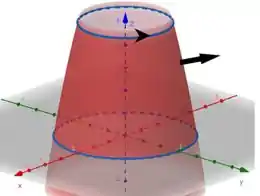
Se a gente anda no sentido anti-horário, como mostra a setinha, a parte vermelhinha da superfície (a parte de fora) fica a nossa direita, não é? Isso o mostra que esse sentido está errado. P
Quando a gente anda na borda, a superfície precisa estar a nossa esquerda. Isso só acontece se andarmos ali no sentido contrário.
Uma outra forma de ver isso é usando a regra da mão direita. Se você coloca seu dedão na direção da setinha, seus outros dedos devem se mover no sentido do vetor normal, furando a superfície de dentro para fora. E não acontece isso ali no caso da figura.
Então esse item também está errado.
Resposta
Letra a