Use o Teorema de Gauss para calcular o fluxo do campo definido por
Através da superfície dada pela equação com , orientada tal que o seu vetor normal tem coordenada negativa.
Passo 1
Como quase todo problema de Teorema de Gauss, é muito legal pra gente iniciar o problema olhando com mais detalhe a superfície de integração que no caso é .
Se a gente trabalhar um pouco com a equação dessa superfície passando o e o pro outro lado...
Ganhamos uma expressão que nos indica que a superfície que a gente está trabalhando aqui se trata de um paraboloide centrada no eixo e virada pra baixo
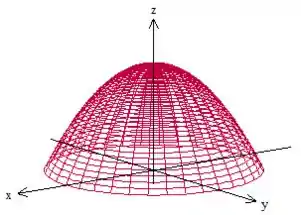
Porém, não estamos interessados em todo o paraboloide, até porque ele cresce infinitamente pra baixo. Só queremos esse pedaço com o
Passo 2
Pois bem... já sabemos que queremos o fluxo do campo através dessa superfície com a normal pra dentro (coordenada negativa), e teremos que fazer isso através de Gauss.
Mas espera! Gauss necessita de uma superfície fechada, correto?
SIM! Mas não é um grande problema pra gente, pois podemos pegar essa ‘tampa’ de baixo ai, ou seja, o plano
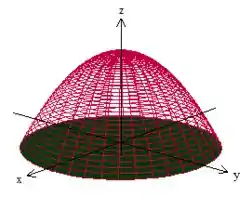
Mas espera novamente! Pra aplicar Gauss precisamos normal pra fora!!!
O que também não é um grande problema, pois depois basta inverter o sinal da resposta que a gente encontrar, beleza?
BELEZA! Então bora aplicar Gauss aí!
Passo 3
é o vetor normal apontando pra fora, como queremos o inverso, basta inverter o sinal da integral tripla
Onde é a superfície fechada que delimita o sólido dentro do paraboloide, ou seja, a união do paraboloide com o plano .
Pela propriedade da soma
Logo, para encontrar o resultado do problema, é procurar a solução das outras duas integrais mais simples. :D
Passo 4
Vamos começar então, por ela: a integral tripla. E começar pela integral tripla, não é nada mais do que começar calculando esse divergente.
Lembre-se que , sendo assim, calculando esses caras e fazendo essa soma
Logo
Veja que maravilha!
Para resolver o problema, basta encontrar uma integral de superfície! :)
Passo 5
Então... calculando essa integral de superfície pelo método direto (não se preocupe, pois ela não será um grande problema. Eu prometo!:D )
Devemos parametrizar a superfície, o que não é um problema, pois estamos em cima de um plano e dentro de uma circunferência, veja só
Logo podemos parametrizar, utilizando coordenadas polares
Como , obtemos a parametrização de
Onde
Vamos agora encontrar o vetor normal, sabendo que .
Calculando essas derivadas parciais aí
Jogando dentro do determinante e resolvendo, vamos obter
Observe que esse vetor é justamente o que queremos, pois ele está apontado pra cima (), ou melhor, pra dentro da superfície.
E aí aqui você precisa ter atenção!! O vetor normal é o vetor que indica a parametrização da superfície! Como ela tem que estar orientada positivamente, ele tem que apontar pra cima! (O que tá ok, porque .)
É diferente do que ele falou no enunciado, que o vetor normal apontava no sentido negativo de . Isso a gente já arrumou quando trocou o sinal do Teorema de Gauss, aqui:
Não confunda!
Passo 6
Agora voltando para a integral
Note que quando fizermos o produto interno desses dois vetores, as duas primeiras coordenas sumirão, logo, devemos mudar para as novas variáveis apenas a terceira coordenada .
Repare também que quando substituirmos as coordenadas, como , apenas restará o , logo
Chegamos em uma integral bem simples, portanto integrando primeiro em e depois em
Passo 7
Voltando para Gauss, temos