Considere a superfície obtida girando-se o segmento de reta que liga os pontos e em torno do eixo . Calcule:
Onde é o campo dos vetores normais exterior a e é um campo vetorial em definido por:
Passo 1
Reparando que os pontos estão ambos no plano , desenhamos a superfície:
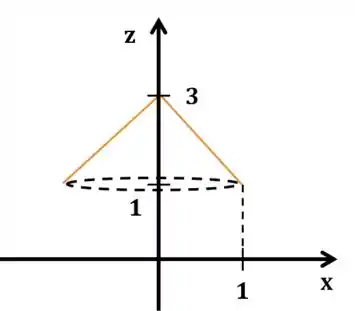
Podemos fecha-la por uma tampa , tal que fechemos o sólido . é definida por:
Passo 2
Calculando o rotacional do campo:
Passo 3
Pelo Teorema de Gauss, sabemos que:
Calculando o divergente de :
Passo 4
Para calcular a integral nova, fazemos uma parametrização da superfície que é a base:
Achando o vetor normal:
Que está apontando para dentro da superfície, como vemos no desenho, portanto trocamos o sinal para respeitar o enunciado e ter um vetor normal exterior:
Passo 5
Substituindo a parametrização na equação de campo e sabendo que a primeira e a segunda coordenadas não influem em nada pois o produto escalar com o normal vai zerar elas:
Substituindo na fórmula, juntamente com os limites de integração da parametrização:
Substituindo na integral que queríamos: