Considere e planos distintos contendo a origem em . Determine :
Passo 1
Bom, eu podia tentar explicar pra vocês usando algum teorema ou relação matemática, mas nesse caso seria um desperdício de tempo. Então nós, malandramente, vamos visualizar o que está acontecendo. Toma uma imagem pra ajudar:
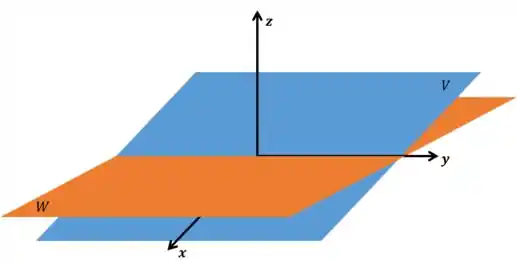
Bom, temos dois planos e distintos do , e ambos esses planos contém a origem.
Bom, só por essa imagem já matamos o problema né? Percebam que de qualquer jeito que você botar os planos, eles vão ter como interseção uma reta! Então a interseção será uma reta passando na origem.
E é isso aí gente, nós se vê por aí.
Resposta
é uma reta que passa na origem.
Exercícios de Livros Relacionados
Dar um sistema de geradores para cada um dos seguintes subespaços do R 3 : U = x , y , x x - 2 y = 0 } V = x , y , x x + z = 0ex - 2 y = 0 } W = x , y , x x + 2 y - 3 z = 0 } U ∩ V V + W
5. Seja a n o número de sequências de “1” e “2” cuja soma dos termos é n. Provar que a n + 1 = a n + a n - 1 . Deduzir a expressão de a n .
Sejam B = { u 1 , u 2 , u 3 } e B ' = v 1 , v 2 , v 3 bases de um espaço vetorial V e P = 2 - 1 3 1 1 4 0 1 2 A matriz de transição de B ' para B Expresse v 1 , v 2 , v 3 como combinação linear de u 1
Sejam B = { u 1 → , u 2 → ,u 3 → } uma base de um espaço vetorial V e T : V → V um operador linear tal que: T B = - 3 4 7 1 0 - 2 0 1 0 Encontre T B ' , sendo B = v 1 → , v 2 → ,v 3 → a base de V defi
Sejam B = { u 1 , u 2 , u 3 } e B ' = v 1 , v 2 , v 3 bases de um espaço vetorial V e P = 2 - 1 3 1 1 4 0 1 2 A matriz de transição de B ' para B Expresse v 1 , v 2 , v 3 como combinação linear de u 1