Considere e planos distintos contendo a origem em . Determine :
Passo 1
Primeiro, podemos escrever uma base para e :
Onde e .
Passo 2
Ta, e agora? Bom, que tal tentarmos visualizar o que está acontecendo? Toma uma imagem pra ajudar:
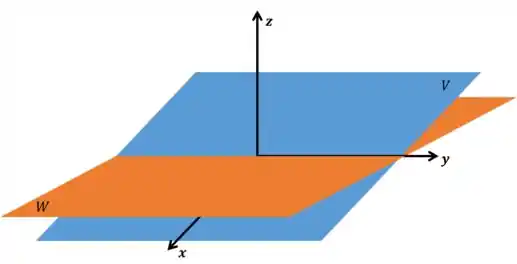
Bom, temos dois planos e distintos do , e ambos esses planos contém a origem.
A primeira e mais importante coisa que temos que notar é que, quaisquer dois planos distintos no que contenham a origem terão sempre uma reta como interseção!
Isso, por sua vez, quer dizer que suas bases poderão ter um vetor em comum, que seria qualquer vetor sobre essa reta!
Sendo assim, podemos dizer que:
Com isso, os planos podem ser escritos como:
Onde é um vetor da reta na qual os planos se interceptam. Por sua vez, é algum outro vetor de e é algum outro vetor de .
Passo 3
Agora que temos uma base para cada um dos planos, podemos encontrar uma base para :
Perceba que e são entre si (caso contrário, e seriam o mesmo plano) e são com relação a (caso contrário, e seriam uma reta).
Sendo assim, o único elemento no conjunto gerador acima é o que aparece duas vezes. Portanto, uma base para seria:
Passo 4
Lembrando que a base contém vetores do , como ela tem elementos, chegamos a conclusão de que:
Resposta