UFPE, Sem campus, Cálculo 3, Listas de Cálculo 3 - UFPE - Integral de Linha, Questão 9b
Calcule , onde
e é a interseção de e , com e , percorrida do ponto ao ponto .
Passo 1
Oiie, tudo bem?
Nós temos que resolver a seguinte integral de linha
em que o campo vetorial dado é tal que
e a curva é a interseção das superfícies
e
com e , percorrendo um sentido tal que saí do ponto e vai até . Integrais de linha podem ser resolvidas pela seguinte definição
em que é uma parametrização da curva. Para visualizarmos quem será a nossa parametrização, vamos realizar a interseção! Ou, se for interessante, podemos usar a seguinte identificação
em que é o vetor normal da superfície orientada tal que é fronteira. Vamos ver o que vale a pena fazer! Vem comigo!
Passo 2
O nosso campo vetorial é tal que
usando a seguinte expressão para calcular o rotacional
calculando as derivadas parciais obtemos
os componentes são apenas constantes, então isso pode facilitar muito nossa vida! Vamos tentar visualizar a curva e a superfície orientada! Saca só!
Passo 3
Temos que a interseção de ambas as superfícies resulta em
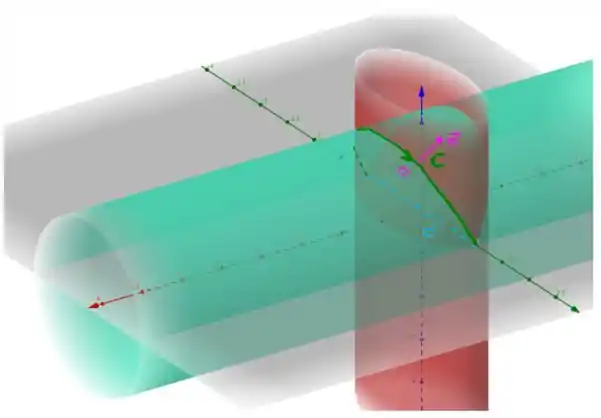
Note que nas condições dadas, temos que a curva é a indicada em verde que parte de e chega em . Mas, a fronteira de nossa superfície ainda requer a curva que anda sobre o eixo de até . De forma, que nossa integral de linha se torna
note que é preciso retirar a contribuição do pedaço da curva que não nos interessa! Vamos tentar achar mais informações sobre a nossa superfície, de maneira que possamos identificar o vetor normal!
Passo 4
Fazendo a interseção das superfícies, temos que
e, portanto, temos que
que é simplesmente
que indica que , que é um plano. Você pode visualizar se rotacionar o gráfico colocando o eixo saindo da tela, da seguinte maneira
Note então que o vetor normal é dado pela equação do plano como
Vamos substituir isso em nossa integral de superfície!
Passo 5
Calculando o produto escalar
temos que a integral de superfície se torna
que é a área de nossa superfície! Vamos tentar visualizar essa região! Se fizermos a interseção do plano com o cilindro , obtemos a equação da elipse novamente
que tem como área simplesmente . Portanto, a integral de superfície é dada por
Note que usei a área , pois temos apenas metade da elipse em . Agora, precisamos calcular a integral de linha da curva para complementar esse resultado! Saca só!
Passo 6
Precisamos de uma parametrização para a curva , ela é uma curva que anda sobre o eixo de até , portanto, ela pode ser parametrizada usando o vetor
E, escolhendo qualquer um dos pontos, temos a parametrização como
A definição de integral de linha é tal que
a derivada de nossa parametrização é simplesmente
O campo vetorial aplicado à minha parametrização é dado por
Portanto, essa integral é simplesmente dada por
pois o produto escalar é zero. O nosso resultado final é então simplesmente dado por
A questão foi isso! Te vejo na próxima! Tchau Tchau!