Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Vetorial no R³

Ver Teoria
Exercício 341234567891011121314151617181920212223242526272829303132333536373839

Enunciado

Integrais de linha – caso vetorial

Calcule ∫ C   F . d r , onde

F x , y , z = y + z , - z , y

E C é a curva obtida com interseção do cilindro x 2 + y 2 = 2 y com o plano y = z .

Passo 1

Antes de mais nada vamos fazer um esboço pra entender o que está acontecendo. Temos um cilindro deslocado no eixo y e um plano:

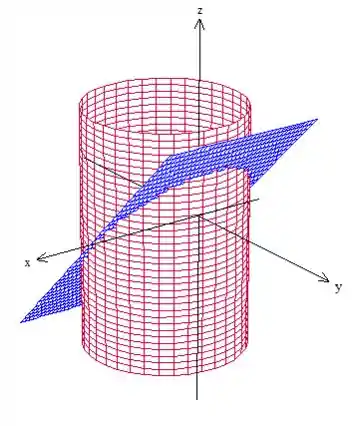
A curva C é formada pela interseção das duas superfícies.

Passo 2

Vamos então parametrizar C . Repare que a projeção da curvan no plano x y é a circunferência de mesma equação que o cilindro:

x 2 + y 2 = 2 y

x 2 + y - 1 2 = 1

Portanto, a parametrização da projeção de C no plano x y é dada, em coordenadas polares deslocadas, por:

( cos ⁡ t ,   s e n   t + 1 )

Show? Mas C é uma curva em três dimensões, tá faltando a coordenada z , que é dada pela equação do plano

z = y

Então, uma parametrização de C seria:

C = ( cos ⁡ t ,   s e n   t + 1 , s e n   t + 1 )

Onde 0 ≤ t ≤ 2 π .

Passo 3

Agora vamos derivar isso aí

C ' = - sen ⁡ t , cos ⁡ t , cos ⁡ t

Passo 4

Show, agora levamos tudo para a fórmula:

∫ C 1   F x , y , z ⋅ d r = ∫ a b F x t ,   y t ⋅ r → ' t d t

O campo é dado por

F x , y , z = y + z , - z , y

Aplicando a parametrização, temos

F x t , y t , z ( t ) = 2 sen ⁡ t + 2 , - sen ⁡ t - 1 , sen ⁡ t + 1

Substituindo então na integral, temos

∫ C   F . d r = ∫ 0 2 π 2 sen ⁡ t + 2 , - sen ⁡ t - 1 , sen ⁡ t + 1 . - sen ⁡ t , cos ⁡ t , cos ⁡ t d t

= ∫ 0 2 π - 2 sen 2 ⁡ t - 2 sen ⁡ t - sen ⁡ t cos ⁡ t - cos ⁡ t + sen ⁡ t cos ⁡ t + cos ⁡ t d t =

= ∫ 0 2 π - 2 sen 2 ⁡ t - 2 sen ⁡ t d t =

Passo 5

Agora é só resolver isso aí. Lembrando que

sen 2 ⁡ t = 1 - cos ⁡ 2 t 2

= ∫ 0 2 π - 2 1 - cos ⁡ 2 t 2 - 2 sen ⁡ t d t =

= ∫ 0 2 π - 1 + cos ⁡ 2 t - 2 sen ⁡ t d t =

= - t + sen ⁡ 2 t 2 + 2 cos ⁡ t 0 2 π =

= - 2 π + sen ⁡ 4 π 2 + 2 cos ⁡ 2 π - - 0 + sen ⁡ 0 2 + 2 cos ⁡ 0 =

= - 2 π + 2 - 2

- 2 π

Resposta

- 2 π

Exercícios de Livros Relacionados

Nos exercícios 18 a 25, calcular as integrais curvilíneas dadas:24. ∫ C y d x + z d y - x y d z , onde C é dada por y = s e nx ; z = 4 ; x ∈ [ 0,2 π ] .
Nos exercícios 18 a 25, calcular as integrais curvilíneas dadas:22. ∫ C d x + d y + d z , onde C é a intersecção das superfícies y + z = 5 e z = 4 - x 2 do ponto A ( 2 ,5 ,0 ) ao ponto B ( - 2 ,5 ,0 )
Calcule ∫ γ d x + x y d y + zd z , onde γ é a interseção de x 2 + y 2 + z 2 = 2 ,x ≥ 0 ,y ≥ 0 e z ≥ 0 , com o plano y = x ; o sentido do percurso é do ponto 0,0 , 2 para 1,1 , 0 .
Calcule a integral de linha ∫ C F → ∙ d r → , onde C é dada pela função vetorial r → t . F → x ,y = x + yi ^ + y - z j ^ + z 2k ^ r → t = t 2i ^ + t 3j ^ + t 2k ^ , 0 ≤ t ≤ 1
Determine uma função f tal que F → = ∇ f e Use a parte (a) para calcular ∫ C F → ⋅ d r → sobre a curva C dada. F → x , y = y 2 c o s c o szi → + 2 x y c o szj → - x y 2 s e nz k → ,C : r → t = t 2 i →