Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Vetorial no R³

Ver Teoria
Exercício 213456789101112131415161718192021222324252627282930313233343536373839

Enunciado

Calcule a integral de linha ∫ C   x + y d x + x y d y + z 2 d z , onde C é a fronteira da parte do plano 2 x + 3 y + z = 12 no primeiro octante.

Passo 1

A gente viu na teoria que para calcular um integral de linha, podemos usar a fórmula:

∫ C F ∙ d r = ∫ a b F x t , y t , z t ∙ σ → ' ( t )   d t

Nós já temos o campo, que vai ser F x , y , z = x + y , x y , z 2 , então só falta parametrizar a curva e encontrar o vetor tangente. Vamos lá!

Passo 2

Ele diz que nossa curva é a fronteira de um plano, então vamos ver qual é essa figura que ele está falando:

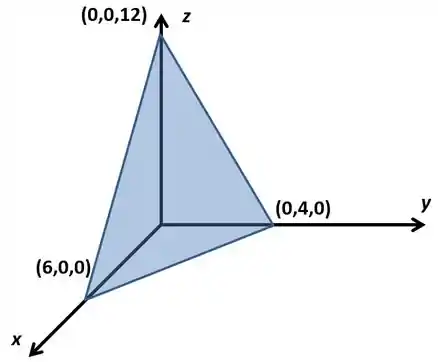
Na real, nossa curva C é o contorno desse triângulo. Então, C é a união de 3 segmentos de reta, consequentemente

∫ C   x + y d x + x y d y + z 2 d z = ∫ C 1   x + y d x + x y d y + z 2 d z + ∫ C 2   x + y d x + x y d y + z 2 d z + ∫ C 3   x + y d x + x y d y + z 2 d z

Passo 3

Mas que segmentos de retas são esses? Olha os pontos onde o plano corta os eixos, vamos ver quando ele corta o eixo x , ou seja, quando z = y = 0

2 x + 0 + 0 = 12

x = 6

Ele passa no ponto 6,0 , 0

Vamos ver quando ele corta o eixo y , ou seja, quando x = z = 0

0 + 3 y + 0 = 12

y = 4

Ele passa no ponto 0,4 , 0

Vamos ver quando ele passa no eixo z , ou seja, quando x = y = 0

0 + 0 + z = 12

z = 12

Ele passa no ponto 0,0 , 12

Vamos fazer a curva C 1 sendo a curva do plano x y quando z = 0 . A curva C 2 sendo a curva do plano x z quando y = 0 . A curva C 3 sendo a curva do plano y z quando x = 0 . Temos que ficar atentos em cada parte para ver a orientação, vamos fazer no sentido anti-horário, ou seja, de 6,0 , 0 até 0,4 , 0 até 0,0 , 12

Passo 4

Vamos começar com a curva C 1

∫ C 1   x + y d x + x y d y + z 2 d z

Precisamos parametrizar esse segmento de reta. Basta pegar a equação do plano e trocar z = 0

2 x + 3 y + 0 = 12

2 x + 3 y = 12

Vamos isolar o x porque é o y que aumenta quando vai de 6,0 , 0 até 0,4 , 0

2 x = 12 - 3 y

x = 6 - 3 2 y

Então, fazendo y = t , vamos ter

σ 1 → = ( 6 - 3 2 t , t , 0 )

Com y indo de 0 à 4 , tendo 0 ≤ t ≤ 4

Passo 5

Agora calculamos σ 1 → ' t :

σ 1 → ' t = d 6 - 3 2 t d t , d t d t , d 0 d t = - 3 2 , 1,0

Passo 6

Vamos, agora, utilizar a fórmula, substituindo o valor de σ 1 → ' y e escrevendo F em função de x :

∫ C 1   F . d r = ∫ a b F x t ,   y t , z t . σ 1 → ' t d t

∫ 0 4 6 - 3 2 t + t , 6 - 3 2 t t , 0 2 ∙ - 3 2 , 1,0 d t =

= ∫ 0 4 6 - 1 2 t , 6 t - 3 2 t 2 , 0 ∙ - 3 2 , 1,0 d t =

= ∫ 0 4 6 - 3 2 - 1 2 - 3 2 t + 6 t - 3 2 t 2 d t =

= ∫ 0 4 - 9 + 3 4 t + 6 t - 3 2 t 2 d t =

= ∫ 0 4 - 9 + 27 4 t - 3 2 t 2 d t =

= - 9 t + 27 4 t 2 2 - 3 2 t 3 3 t = 0 4 =

= - 9 t + 27 t 2 8 - t 3 2 t = 0 4 =

= - 9 ∙ 4 + 27 ∙ 4 2 8 - 4 3 2 - - 9 ∙ 0 + 27 ∙ 0 2 8 - 0 3 2

= - 36 + 27 ∙ 16 8 - 64 2 - 0

= - 36 + 54 - 32

= - 14

Passo 7

Vamos ver a segunda agora

∫ C 2   x + y d x + x y d y + z 2 d z

Precisamos parametrizar esse segmento de reta. Basta pegar a equação do plano e trocar y = 0

2 x + 0 + z = 12

2 x + z = 12

Vamos isolar o z porque é o x que aumenta quando vai de 0,0 , 12 até 6,0 , 0

z = 12 - 2 x

Fazendo x = t :

σ 2 → = ( t , 0 , 12 - 2 t )

Com x indo de 0 à 6 , tendo 0 ≤ t ≤ 6

Passo 8

Agora calculamos σ 2 → ' t :

σ 2 → ' t = d t d t , d 0 d t , d 12 - 2 t d t = 1,0 , - 2

Passo 9

Vamos, agora, utilizar a fórmula, substituindo o valor de σ 2 → ' x e escrevendo F em função de x :

∫ C 2   F . d r = ∫ a b F x t ,   y t , z t . σ 2 → ' t d t

∫ 0 6 t + 0 , t ∙ 0 , 12 - 2 t 2 ∙ 1,0 , - 2 d t =

= ∫ 0 6 t , 0,144 - 48 t + 4 t 2 ∙ 1,0 , - 2 d t =

= ∫ 0 6 t - 288 + 96 t - 8 t 2 d t =

= ∫ 0 6 - 288 + 97 t - 8 t 2 d t =

= 97 t 2 2 - 288 t - 8 t 3 3 t = 0 6 =

= 97 ∙ 6 2 2 - 288 ∙ 6 - 8 ∙ 6 3 3 - 97 ∙ 0 2 2 - 288 ∙ 0 - 8 ∙ 0 3 3

- 558

Nossa, quanta conta... Mas não perde o ânimo não que só falta uma!

Passo 10

Vamos ver a terceira agora

∫ C 3   x + y d x + x y d y + z 2 d z

Precisamos parametrizar esse segmento de reta. Basta pegar a equação do plano e trocar x = 0

0 + 3 y + z = 12

3 y + z = 12

Vamos isolar o y porque é o z que aumenta quando vai de 0,4 , 0 até 0,0 , 12

3 y = 12 - z

y = 4 - z 3

De novo, vamos fazer z = t :

σ 3 → = 0 , 4 - t 3 , t

Com z indo de 0 à 12 , tendo 0 ≤ t ≤ 12

Passo 11

Agora calculamos σ 3 → ' t :

σ 3 → ' t = d 0 d t , d 4 - t 3 d t , d t d t = 0 , - 1 3 , 1

Passo 12

Vamos, agora, utilizar a fórmula, substituindo o valor de σ 3 → ' t e escrevendo F em função de t :

∫ C 3   F . d r = ∫ a b F x t ,   y t , z t . σ 3 → ' t d t

∫ 0 12 0 + 4 - t 3 , 0 ∙ 4 - t 3 , t 2 ∙ 0 , - 1 3 , 1 d t =

= ∫ 0 12 4 - t 3 , 0 , t 2 ∙ 0 , - 1 3 , 1 d t =

= ∫ 0 12 t 2 d t =

= t 3 3 t = 0 12 =

= 12 3 3 - 0 3 3

= 576

Passo 13

Finalmente, agora que temos as 3 integrais, é só substituir

∫ C   x + y d x + x y d y + z 2 d z = ∫ C 1   x + y d x + x y d y + z 2 d z + ∫ C 2   x + y d x + x y d y + z 2 d z + ∫ C 3   x + y d x + x y d y + z 2 d z

∫ C   x + y d x + x y d y + z 2 d z = - 14 - 558 + 576 = 4

Resposta

4

Exercícios de Livros Relacionados

Nos exercícios 18 a 25, calcular as integrais curvilíneas dadas:24. ∫ C y d x + z d y - x y d z , onde C é dada por y = s e nx ; z = 4 ; x ∈ [ 0,2 π ] .
Nos exercícios 18 a 25, calcular as integrais curvilíneas dadas:22. ∫ C d x + d y + d z , onde C é a intersecção das superfícies y + z = 5 e z = 4 - x 2 do ponto A ( 2 ,5 ,0 ) ao ponto B ( - 2 ,5 ,0 )
Calcule ∫ γ d x + x y d y + zd z , onde γ é a interseção de x 2 + y 2 + z 2 = 2 ,x ≥ 0 ,y ≥ 0 e z ≥ 0 , com o plano y = x ; o sentido do percurso é do ponto 0,0 , 2 para 1,1 , 0 .
Calcule a integral de linha ∫ C F → ∙ d r → , onde C é dada pela função vetorial r → t . F → x ,y = x + yi ^ + y - z j ^ + z 2k ^ r → t = t 2i ^ + t 3j ^ + t 2k ^ , 0 ≤ t ≤ 1
Determine uma função f tal que F → = ∇ f e Use a parte (a) para calcular ∫ C F → ⋅ d r → sobre a curva C dada. F → x , y = y 2 c o s c o szi → + 2 x y c o szj → - x y 2 s e nz k → ,C : r → t = t 2 i →