Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Caso Vetorial no R³

Ver Teoria
Exercício 351234567891011121314151617181920212223242526272829303132333436373839

Enunciado

Seja a curva parametrizada:

α t = cos ⁡ t , sin ⁡ t ,   1 + cos 2 ⁡ t ,   t ∈ - 3 π 4 ,   0 .

  1. Calcule equações implícitas para α .
  2. Faça um esboço da imagem de α .
  3. Calcule as equações implícitas da reta tangente a α em - π 2 .
  4. Calcule a integral de linha

∫ α   16 x 3 y - y 3 x d s

Passo 1

Letra a) cara, nesse tipo de problema, a primeira coisa sem dúvida que devemos fazer é nomear cada entrada da parametrização das coordenadas cartesianas, assim oh

α t = cos ⁡ t ⏟ x , sin ⁡ t ⏟ y ,   1 + cos 2 ⁡ t ⏟ z

Então a gente terá

x = cos ⁡ t

y = sin ⁡ t

z = 1 + cos 2 ⁡ t

beleza?

Passo 2

Bem, agora o que a gente vai tentar fazer é associar essas três coisas umas com as outras. Lembre-se: o nosso principal objetivo aqui é eliminar o t !

Veja, que dali a gente consegue tirar uma relação direta:

Como x = cos ⁡ t ... substituindo na equação de baixo...

z = 1 + cos 2 ⁡ t     →                 z = 1 + x 2

Será que acabou?

Não! Não acabou, porque se você se lembrar, precisamos de duas equações cartesianas para definir uma curva no espaço, beleza?

Beleza! Mas onde está a outra curva?

Passo 3

Então, para a outra curva, a gente tem que utilizar a segunda informação que não utilizamos ainda: y = sin ⁡ t

Pow! O cosseno e o seno tem uma relação fundamental:

cos 2 ⁡ t + sin 2 ⁡ t = 1

EPA! Agora é só substituir com a primeira equação x = cos ⁡ t !

cos 2 ⁡ t + sin 2 ⁡ t = 1         →                 y 2 + x 2 = 1

Logo, as duas equações que definem a curva no espaço é

y 2 + x 2 = 1 z = 1 + x 2

Passo 4

Letra b) pow, pra gente desenhar a curva aqui, vamos entender primeiro o que que essas equações significa no espaço?

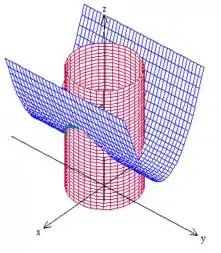
Bem, a primeira delas, y 2 + x 2 = 1 , a gente já viu que forma pra gente um cilindro centrado no eixo z :

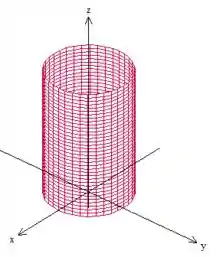
Quanto à outra superfície, z = 1 + x 2 , bem... Vamos ver como é essa equação primeiro no plano x z :

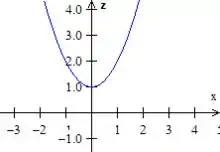
Como a gente está no espaço agora, temos que acrescentar o y . Mas EPA! essa equação não depende de y , então vamos apenas...

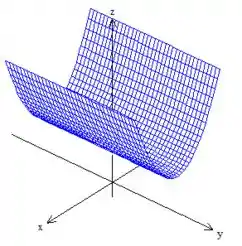
puxar essa parábola em torno de y , viu?

Passo 5

Colocando agora essas duas superfícies juntas...

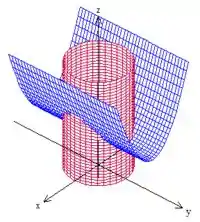
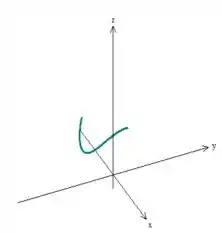
conseguimos ver a curva na intersecção das duas

Mas cuidado! Não queremos toda a curva, só queremos a que satisfaz   t ∈ - 3 π 4 ,   0 .

Como o ângulo t varia em cima do eixo x no sentido horário positivo, dessa forma aqui

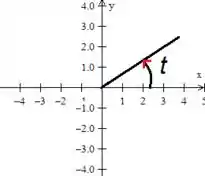
Então ao ângulo negativo significa voltar, teremos que voltar um total de 3 π 4   r a d 135 º     : D

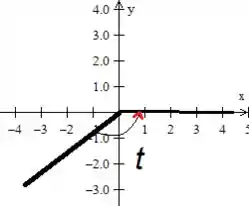
Comparando com as superfícies ali em cima, a gente percebe que a curva α então na verdade, é:

Passo 6

Letra c) a primeira coisa que nos devemos perguntar aqui é: qual é a forma de uma reta parametrizada mesmo?

Bem, lá da álgebra vimos que se tivermos um vetor tangente V = ( A ,   B ,   C ) e o ponto P = x 0 ,   y 0 ,   z 0 onde a gente quer, a gente consegue a reta paramétrica, pela relação:

x = x 0 + A t y = y 0 + B t z = z 0 + C t

O legal é que o ponto P a gente já tem, basta substituir t = - π 2 na equação da curva (o ponto tangente também está na curva, tá ligado?)

α t = cos ⁡ t , sin ⁡ t ,   1 + cos 2 ⁡ t     →

α - π 2 = cos ⁡ - π 2 , sin ⁡ - π 2 ,   1 + cos 2 ⁡ - π 2     →

Calculando esses senos e cossenos...

α - π 2 = 0 , - 1 ,   1     →                 x 0 = 0 y 0 = - 1 z 0 = 1

Substituindo então o ponto P

x = 0 + A t y = - 1 + B t z = 1 + C t

Agora para o vetor tangente V , vem comigo!

Passo 7

Lembra-se de que se o problema nos dá uma curva, podemos facilmente obter os vetores tangentes a ela? Basta derivar a curva, não é mesmo?

Veja só: α t = cos ⁡ t , sin ⁡ t ,   1 + cos 2 ⁡ t

Derivando cada termo em relação a t (não esqueça de aplicar a regra da cadeia em 1 + cos 2 ⁡ t , ok?

α ' t = - sin ⁡ t , cos ⁡ t , - 2 cos ⁡ t ∙ sin ⁡ t

Bem, como a reta é tangente à curva, o vetor tangente V que queremos é o vetor no ponto de interesse t = - π 4 !!!

Substituindo no vetor tangente

t = - π 2         ⇒             α ' - π 2 = - sin ⁡ - π 2 , cos ⁡ - π 2 , - 2 cos ⁡ - π 2 ∙ sin ⁡ - π 2 →

α ' - π 2 = - - 1   ,   0   ,   - 2 0 ∙ - 1 →

α ' - π 2 = 1   ,   0   ,   0

Logo,

x = 0 + A t y = - 1 + B t z = 1 + C t                       →             ��             x = t y = - 1 z = 1

Passo 8

Letra d) Então...

∫ α   16 x 3 y - y 3 x d s

para calcular essa integral de linha, vai ser easy! Por quê?

Ué, pois já temos quase tudo pronto.

Passo 9

Para calcular essa integral de linha, vamos primeiro substituir o d s . Como? Ora:

d s = α ' ( t ) d t

A gente já tem esse α ' ( t ) : α ' t = - sin ⁡ t , cos ⁡ t , - 2 cos ⁡ t ∙ sin ⁡ t

Logo

α ' t = - sin ⁡ t 2 + cos ⁡ t 2 + - 2 cos ⁡ t ∙ sin ⁡ t 2 →

d s = sin 2 ⁡ t + cos 2 ⁡ t + 4 cos 2 ⁡ t ∙ sin 2 ⁡ t   d t →

Já vimos que sin 2 ⁡ t + cos 2 ⁡ t vale 1 , então

d s = 1 + 4 cos 2 ⁡ t ∙ sin 2 ⁡ t   d t

Passo 10

Substituindo na integral...

∫ α   16 x 3 y - y 3 x d s = ∫     16 x 3 y - y 3 x 1 + 4 cos 2 ⁡ t ∙ sin 2 ⁡ t   d t

Como vamos integrar em t , vamos substituir α pelo limite de t ,

∫ - 3 π 4   0   16 x 3 y - y 3 x 1 + 4 cos 2 ⁡ t ∙ sin 2 ⁡ t   d t

Observe que dentro dos parênteses, podemos colocar em evidência o x y , certo?

∫ - 3 π 4   0   16 x y x 2 - y 2 1 + 4 cos 2 ⁡ t ∙ sin 2 ⁡ t   d t

Além disso, trocar x , y e z pelos parâmetros que vimos no passo 2

∫ - 3 π 4   0   16 cos ⁡ t ∙ sin ⁡ t cos 2 ⁡ t - sin 2 ⁡ t 1 + 4 cos 2 ⁡ t ∙ sin 2 ⁡ t   d t

Putz! Que integral escrota! Cara, temos que melhorar isso aí, mas nota o seguinte:

Lembra-se de arcos duplos lá da trigonometria?

sin ⁡ 2 t = 2 cos ⁡ t ∙ sin ⁡ t

cos ⁡ 2 t = cos 2 ⁡ t - sin 2 ⁡ t

EPA! É exatamente o que temos ali (inclusive aquele termo dentro da raiz )

Então podemos substituir tudo. Veja só

∫ - 3 π 4   0   8 ∙ 2 cos ⁡ t ∙ sin ⁡ t cos 2 ⁡ t - sin 2 ⁡ t 1 + 2 cos ⁡ t ∙ sin ⁡ t 2   d t     →

∫ - 3 π 4   0   8 ∙ sin ⁡ 2 t cos ⁡ 2 t 1 + sin �� 2 t 2   d t

Bem melhor neh? Vamos partir para a integral então!

Passo 11

Pow, queremos resolver essa integral. Como a gente tem um termo dentro da raiz, a primeira coisa que temos que pensar então é uma substituição simples. Será que vai simplificar a nossa vida? Vejamos

∫ - 3 π 4   0   8 ∙ sin ⁡ 2 t cos ⁡ 2 t 1 + sin ⁡ 2 t 2   d t

Se substituirmos 1 + sin ⁡ 2 t 2 por uma variável qualquer

1 + sin ⁡ 2 t 2 = a

o d a , será (cuidado com a regra da cadeia)

d a = 2 sin ⁡ 2 t cos ⁡ 2 t �� 2   d t

Cara, é exatamente o que temos do lado de fora! Então realmente é assim que devemos matar a questão, percebeu?

∫ - 3 π 4   0   8 ∙ sin ⁡ 2 t cos ⁡ 2 t 1 + sin ⁡ 2 t 2   d t = ∫       2 a   d a

Bem, mas toda mudança precisamos determinar os novos limites...

t = - 3 π 4             →             a = 1 + sin ⁡ 2 - 3 π 4 2 = 1 + sin ⁡ - 3 π 2 2   →

Lembrando que sin ⁡ - 3 π 2 = 0

a = 1 + 0 = 1

Por outro lado...

t =             →             a = 1 + sin ⁡ 2 0 2 = 1 + sin ⁡ 0 2

a = 1 + 1 = 2

Logo... substituindo...

∫ 2     1   2 a   d a =

integrando...

2 a 3 2 3 2 2 1 =

2 2 a 3 2 3 2 1 =

2 2 3 - 2 ∙ 2 3 2 3

Como 2 3 2 = 2 3 = 2 2

2 2 3 - 4 2 3 = 4 3 - 8 2 3

Resposta

Letra a)

y 2 + x 2 = 1 z = 1 + x 2

Letra b)

Letra c)

x = t y = - 1 z = 1

Letra d)

4 3 - 8 2 3

Exercícios de Livros Relacionados

Nos exercícios 18 a 25, calcular as integrais curvilíneas dadas:24. ∫ C y d x + z d y - x y d z , onde C é dada por y = s e nx ; z = 4 ; x ∈ [ 0,2 π ] .
Nos exercícios 18 a 25, calcular as integrais curvilíneas dadas:22. ∫ C d x + d y + d z , onde C é a intersecção das superfícies y + z = 5 e z = 4 - x 2 do ponto A ( 2 ,5 ,0 ) ao ponto B ( - 2 ,5 ,0 )
Calcule ∫ γ d x + x y d y + zd z , onde γ é a interseção de x 2 + y 2 + z 2 = 2 ,x ≥ 0 ,y ≥ 0 e z ≥ 0 , com o plano y = x ; o sentido do percurso é do ponto 0,0 , 2 para 1,1 , 0 .
Calcule a integral de linha ∫ C F → ∙ d r → , onde C é dada pela função vetorial r → t . F → x ,y = x + yi ^ + y - z j ^ + z 2k ^ r → t = t 2i ^ + t 3j ^ + t 2k ^ , 0 ≤ t ≤ 1
Determine uma função f tal que F → = ∇ f e Use a parte (a) para calcular ∫ C F → ⋅ d r → sobre a curva C dada. F → x , y = y 2 c o s c o szi → + 2 x y c o szj → - x y 2 s e nz k → ,C : r → t = t 2 i →