Integrais de linha – caso vetorial
Calcule sendo a curva dada pela interseção das superfícies e , percorrida de a
Passo 1
Bom, antes de tudo precisamos parametrizar essa curva né? Sabemos que ela é dada pela interseção entre as superfícies:
A primeira se trata de um hiperboloide de uma folha com simetria no eixo , enquanto a segunda é um plano. Temos algo assim:
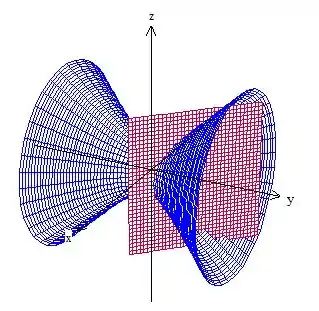
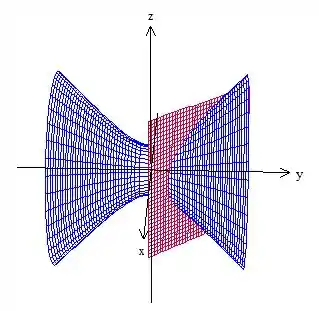
A curva é então a interseção dessas duas superfícies. Vamos substituir uma equação na outra então:
Vamos então usar como parâmetro, ok? Temos:
Isso nos dá a seguinte parametrização:
Como o enunciado diz que a curva é percorrida de a , temos .
Passo 2
Vamos, agora, calcular :
Passo 3
Podemos, então, substituir na fórmula abaixo, escrevendo o campo em função da nossa parametrização:
O campo
Fica
Isso nos dá
Repare que o intervalo da integral é aquele que encontramos para na parametrização!
Passo 4
Agora falta resolver a integral né?
Vamos resolver primeiro a segunda integral
Agora precisamos fazer essa integração por partes, temos:
Aplicando a fórmula
Temos