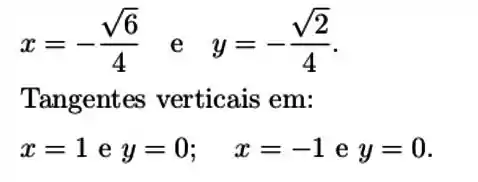Passo 1
Vamos entender algo importante: as retas tangentes horizontais terão coeficiente angular valendo , ou seja, . Para as verticais, teremos o coeficiente angular infinito. Vamos derivar a função implicitamente e descobrir aonde assume esses valores:
Passo 2
Vamos zerar o numerador para achar onde a derivada é nula, ou seja, onde temos as tangentes horizontais:
Repare, não é uma solução pois o ponto onde é a origem, com . Nesse ponto, vemos no gráfico que a derivada não é nula, além de que a fórmula de ficaria com uma indeterminação de em sua expressão.
Enfim, vamos procurar o seguinte:
Passo 3
Então, aplicando essa relação na função da lemniscata:
Passo 4
Então, acharemos para :
Portanto, os pontos serão:
Passo 5
Procuramos agora os pontos onde vai explodir para . Devemos então zerar o denominador desse cara:
Repara, o termo do parênteses é uma soma de termos de expoente par, que são sempre positivos, e uma constante positiva. Esse cara nunca vai ser zero. Assim, tudo depende do .
Passo 6
E quando isso acontece na função dada? Vamos aplicar na sua equação e descobrir:
Como já falamos antes, o ponto e não nos interessa, pois não vai gerar a reta vertical tangente. Então, ficamos com:
Os pontos serão, portanto:
Resposta