Exercícios Resolvidos de Derivação Implícita

Exercício 19 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

Enunciado

Lista 2.8 – Derivada de função implícita – UFSC – Cálculo 1 – Questão C5

Um homem anda ao longo de um caminho reto no plano, sobre o eixo e no sentido positivo, a uma velocidade de . Um holofote, que está localizado sobre o eixo positivo a da origem, focaliza o homem. Seja o menor ângulo que o holofote faz com o eixo . Qual é a derivada em relação ao tempo de quando o homem está a da origem?

Passo 1

Falaee, beleza?? Seguinte... vamos primeiramente tentar enxergar o que a questão está nos dizendo com uma figura. Se liga aí:

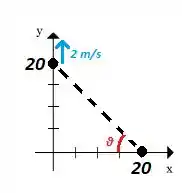
Passo 2

Pela figura, podemos tirar algumas informações:

Em que, para , temos:

Passo 3

Além disso, a gente sabe que a derivação é implícita quando a variável dependente não está isolada, certinho?

Dessa forma, a gente deriva os dois lados da igualdade para descobrirmos o resultado da derivada!!

Assim, olha:

Passo 4

Sendo e , temos:

Entendeu direitinho? Responde aee ;)

Resposta

Exercícios de Livros Relacionados

14. Seja z = t 2 f ( x , y ) , onde x = t 2 e y = t 3 . Expresse d z d t em termos das derivadas parciais de f .

18. Seja g ( x ) uma função diferenciável tal que f x ,g x = 0 , para todo x ∈ D g . Mostre que g ' x = - ∂ f ∂ x x ,g x ∂ f ∂ y x ,g x Para todo x ∈ D g , com ∂ f ∂ y x ,g x ≠ 0 .

Use a derivação implícita para determinar ∂ z / ∂ x e ∂ z / ∂ y . x 2 + y 2 + z 2 = 3 x y z

20. f ( x , y , z ) e g ( x , y ) são funções diferenciáveis tais que, para todo ( x , y ) no domínio de g . f x , y ,g x , y = 0 . Suponha g 1,1 = 3 , ∂ f ∂ x 1,1 , 3 = 2 , ∂ f ∂ y 1,1 , 3 = 5 e ∂ f

Seja f x , y diferenciável em R 2 e tal que para todo ( x , y ) ∂ f ∂ x + ∂ f ∂ y = 0 Verifique que a função g u , v dada por f ( x , y ) , onde x = u + v e y = u é tal que ∂ g ∂ u = 0 .. Conclua que