Seja um oscilador harmônico forçado, com amortecimento sub-crítico, onde e representam massa, constante de mola e coeficiente de atrito, respectivimente. A força externa é ligada em quando o oscilador está na posição e tem velocidade .
Tomando como a direção de vibração do oscilador, obtenha a partir do balanço das forças a equação do movimento (equação diferencial em , e ).
Encontre a solução transitória do movimento.
Deduza a solução estacionária do movimento, indicando amplitude e defasagem em relação à força externa aplicada.
Escreva a solução geral do movimento (transitória + estacionária) em termos das condições iniciais, e .
Passo 1
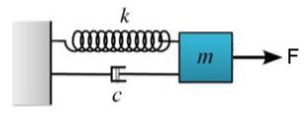
Esse sistema se caracteriza como uma oscilação amortecida forçada, com força oscilatória, pois como a força é multiplicada pelo a força vai variar com o tempo. Podemos esquematizar esse sistema assim:
Se isolarmos esse sistema observamos a ação dessas forças
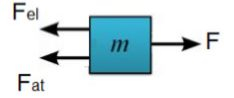
Assim, podemos escrever a equação da força resultante
Agora podemos abrir cada uma dessas forças. A equação da força elástica e de atrito já sabemos bem, e a força resultante podemos escrevê-la usando a lei de Newton e por fim a força que o enunciado nos deu a equação:
Então nossa equação da força resultante no sistema é
Já estamos quase no fim, só temos que lembrar que a derivada da posição é a velocidade e a derivada da velocidade é a aceleração, então:
Agora, podemos rescrever tudo em função de e suas derivadas
Passando tudo que tem para um lado, chegamos na equação diferencial geral de um movimento oscilatório forçado, com força externa oscilatória.
Já encontramos a equação diferencial do movimento, mas podemos deixa-la mais limpa, não só para agradar os professores, mas para simplificar as constantes e nos ajudar no futuro. Para isso vamos dividir toda a equação pela massa
E por último vamos chamar
Assim, chegamos no resultado final
Passo 2
Agora temos que resolver essa equação, vamos ter que brincar com o calculo, moleza para você, aporto! :D
Queremos encontrar a equação transitória da EDO que acabamos de encontrar:
Como queremos a solução transitória, como transitório é aquele momento em que a solução particular tende a zero. Então para achar a solução transitória basta resolver
O que torna nosso trabalho bem mais fácil, pois achar a solução particular é trabalhoso, quase impossível.
Então vamos começar a resolver, primeiro passo será escrever o polinômio característico da EDO.
Agora, vamos lembrar que o enunciado nos disse que o amortecimento é sub-crítico, isso quer dizer que
este que que vale
A solução do polinômio é:
Como o é negativo, significa que teremos uma solução imaginaria. Assim usaremos o número imaginário para continuar as contas, pois
Como a solução é imaginária, podemos separar ela em parte real e parte imaginaria
Escrevendo desta forma, temos
Assim:
A solução de uma EDO, onde o é negativo é da seguinte forma
Vamos escrever nossa solução então
Agora, vamos simplificar isso novamente! Para isso usaremos uma variável
Então, nossa solução fica da forma
Passo 3
A solução estacionaria é aquela que não depende do tempo, e nela a oscilação terá a mesma frequência da força externa.
Na teoria vimos que quando isso acontece temos que a solução da EDO será dada apenas pela solução particular
Onde e são funções de a serem determinadas.
Para isso temos que substituir na EDO:
Isolando
Passo 4
Agora precisamos simplificar essa equação e para isso vamos usar as relações trigonométricas.
Usando que :
Assim:
Isso que você chama simplificar?? Calma, ficou mais feio, mas é por uma boa causa hahaha! Bora lá!
Vamos isolar :
Agora podemos cortar o e chegamos em uma equação assim:
Agora podemos colocar o em evidencia
Podemos reescrever isso substituindo por
Agora, vamos usar o fato que a solução que queremos é a estacionária, isso quer dizer que a solução não pode depender do tempo então onde tem o de tempo deverá zerar para que a solução não dependa do tempo. Então vamos separar tudo que depende do tempo e igualar a zero.
Daqui podemos cortar e chegamos em
Agora conseguimos isolar
Podemos inverter isso e dizer que
Assim, o valor de será
Isso para uma defasagem de zero . Se escolhermos uma defasagem de por exemplo temos que
Então chegaríamos em
E
Isso depende da defasagem que você escolher.
Passo 5
Agora que descobrimos quanto vale o ângulo em função de , falta apenas descobrir a função para a amplitude .
Voltando a equação que encontramos
Já vimos que para ser estacionaria os termos que dependem do tempo vão sumir assim, só vai restar:
Isolando a Amplitude que é o de precisamos descobri
Lembra que achamos esse valor para , considerando a fase igual a zero.
Como tangente pode ser escrita como a razão entre seno e cosseno
Então o cosseno é
Então substituindo isso, temos:
Simplificando a equação temos
Beleza, muita conta eu sei! Mas já estamos no fim, não desiste não!
Agora precisamos só simplificar isso, a resposta você já achou, só precisa simplificar para garantir o dez.
Se você observar a parte que multiplica a massa temos:
Que podemos pensar em um quadrado perfeito, se olharmos assim:
Viu?!!
Então chegamos que a amplitude vale:
Por fim, podemos colocar o inverter com para sumir com os sinais de menos
Boa, chegamos ao fim da resposta desse item, porque conseguimos definir a amplitude e o valor de , assim a solução será
Onde:
Passo 6
Queremos encontrar a solução geral da EDO.
A solução geral de uma EDO não homogênea é dada pela soma da solução homogênea com a particular.
A particular a gente terminou de determinar no item , e a solução homogênea encontramos no item , mas ela não está completamente definida, pois falta definirmos as constantes e
E para isso vamos usar as situações de contorno e
A primeira condição de contorno nos diz que a solução quando é
Como
Assim,
Agora analisando a segunda condição temos que
Onde
Como
E a derivada de é
Para , temos:
O sen vale:
Então o valor de será:
Vamos voltar ao calculo de
Substituindo o valor de
Isolando , temos
Substituindo e temos:
É amigo, essa é a resposta final, demorou, mas chegamos lá!
Resposta
;
Onde:
; ;
Solução geral: