Um oscilador harmônico forçado é descrito por uma equação de movimento dada por:
![]()
O quadrado da amplitude de oscilação (normalizada pelo seu valor máximo) em função da frequência angular da força aplicada é dada pelo gráfico ao lado:
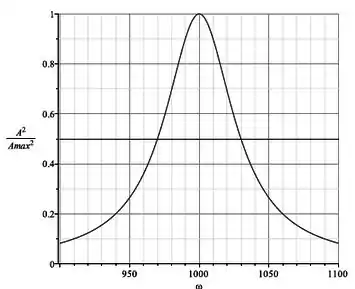
Se a massa do corpo é de 1 kg, responda:
a) Qual o valor da constante k da força de restauro?
b) Qual o valor da constante da força de restauro?
c) Se em um dado instante t = 0 a força externa for desligada, qual a função x(t) que descreve a posição da massa?
Passo 1
Eiiii presta atenção aqui que essa questão tem um treco que parece complicado, mas não é.
Quando ele dá o gráfico do quadrado da amplitude assim, geralmente estamos falando de fator de qualidade ou mérito. A gente chama esse cara de Q, e escreve assim:
Em que é a frequência para amplitude máxima e é a largura de banda. É a largura do gráfico quando .
No caso dessa questão:
E como:
Beleza! Isso tudo que eu acabei de te falar só é válido pra amortecimentos muito pequenos.
Na frequência de ressonância, , para amortecimentos pequenos.
A ressonância acontece no pico. Então na ressonância:
E fazendo:
O amortecimento de fato é muito pequeno e as aproximações estão corretas. Show!
Passo 2
Como nós já achamos que podemos fazer:
Passo 3
b) Sabemos que:
Substituindo:
Passo 4
c) Se a força externa for desligada, teremos um MHA normalzinho.
O regime de amortecimento vai ser o subcrítico, como vimos no item a.
A solução do regime subcrítico é:
Vamos calcular :
Então:
Como não foi dada nenhuma condição inicial, o A e o ficam desse jeitinho aí mesmo.
Resposta
a)
b)
c)