UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo de Várias Variáveis - Lista 2 - Integral de Linha, Questão 2.2.3e
Calcule as seguintes integrais de linha ao longo do caminho indicado:
e)
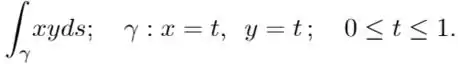
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para determinar do resultado da seguinte integral de linha:
Lembrando que seu caminho é dado por:
Onde .
Para resolver esse problema temos que parametrizar a curva em termos de e depois aplicar na integral.
E aí? Bora lá?
😉
Passo 2
Dessa forma, parametrizando a curva, temos:
Onde está no intervalo .
Agora, vamos calcular as diferenciais e e termos de :
Nesse sentido, vamos calcular o elemento de comprimento em termos de e :
Assim, substituindo as expressões para e na integral de linha, temos:
Passo 3
Por fim, podemos resolver a integral que acabamos de encontrar:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Como se calcula a área de uma superfície parametrizada no espa-ço? E de uma superfície implicitamente definida F(x, y, z) = 0?E da superfície que é o gráfico de z = ƒ(x, y)? Dê exemplos
Calcule 1C F ∙ T ds para o campo vetorial F = x2i – yj ao longoda curva x = y2 de (4, 2) a (1, –1).
Calcule int_C x y d x + ( x + y ) d y ao longo da curva y = x^2 de ( - 1,1 ) a ( 2,4 )
O que são integrais de linha? Como elas são calculadas? Dêexemplos
Calcule as integrais nos Exercícios 9 e 10.10. ∫ y 2d x + x 2d x C é a circunferência x 2 + y 2 = 4 .