Listas de Física 3 - UFRJ de Física 3 da UFRJ - Lista 1 - Carga Elétrica e Campo Elétrico

Duas esferas idênticas, cada uma com massa , são suspensas por fios ideais e isolantes de comprimento , como indicado na figura abaixo. Elas possuem cargas de mesmo módulo e sinais opostos e estão sob a ação de um campo elétrico uniforme , de direção horizontal e intensidade desconhecida, e do campo gravitacional . Quando o sistema está em equilíbrio, o ângulo que os fios fazem com a vertical vale . Nessas condições, determine:

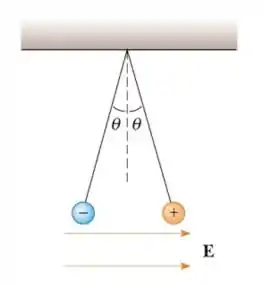
1. A tensão no fio

Duas esferas idênticas, cada uma com massa , são suspensas por fios ideais e isolantes de comprimento , como indicado na figura abaixo. Elas possuem cargas de mesmo módulo e sinais opostos e estão sob a ação de um campo elétrico uniforme , de direção horizontal e intensidade desconhecida, e do campo gravitacional . Quando o sistema está em equilíbrio, o ângulo que os fios fazem com a vertical vale . Nessas condições, determine:

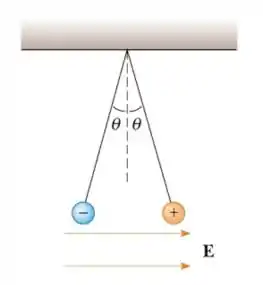
b) A intensidade do campo elétrico.

Três cargas puntiformes − e são posicionadas sobre os vértices de um triângulo equilátero de lado a, como indicado na figura abaixo.

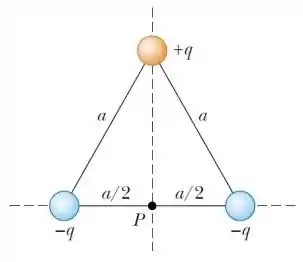
1. Determine o vetor campo elétrico no ponto P indicado na figura

Três cargas puntiformes − e são posicionadas sobre os vértices de um triângulo equilátero de lado a, como indicado na figura abaixo.

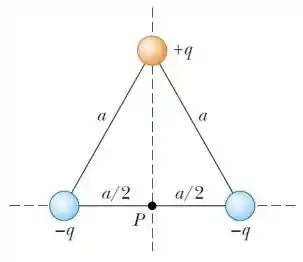
(b) Determine o vetor campo elétrico no centro do triângulo.

Três cargas puntiformes − e são posicionadas sobre os vértices de um triângulo equilátero de lado a, como indicado na figura abaixo.

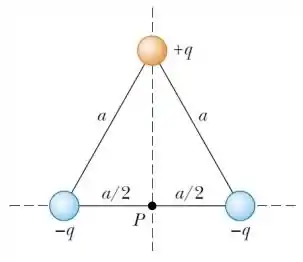
(c) Determine o vetor força elétrica resultante sobre uma das cargas .

Uma linha isolante de cargas tem a forma de um semicírculo de raio , como indicado na figura abaixo. Sua densidade linear de carga é dada por , onde é uma constante positiva e é o ângulo polar medido a partir do eixo .

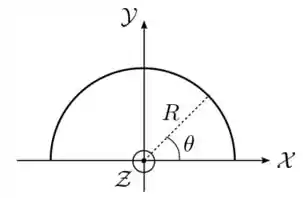
(a) Determine a carga total contida na linha.

Uma linha isolante de cargas tem a forma de um semicírculo de raio , como indicado na figura abaixo. Sua densidade linear de carga é dada por , onde é uma constante positiva e é o ângulo polar medido a partir do eixo .

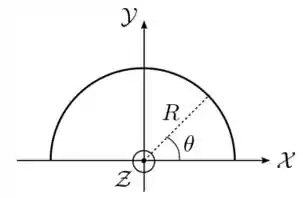
(b) Determine o vetor campo elétrico no centro do semicírculo.

Uma linha isolante de cargas tem a forma de um semicírculo de raio , como indicado na figura abaixo. Sua densidade linear de carga é dada por , onde é uma constante positiva e é o ângulo polar medido a partir do eixo .

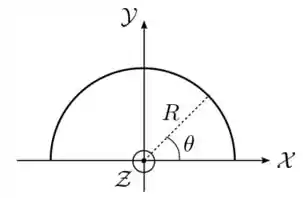
(c) Repita os dois itens acima, mas supondo agora que .

Três cargas puntiformes e são posicionadas ao longo do eixo de um sistema de coordenadas, como indicado na figura abaixo. A separação entre duas cargas adjacentes vale .

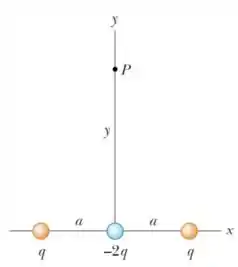
1. Determine o vetor campo elétrico em um ponto localizado sobre o eixo , a uma distância da origem, como indicado na figura.

1. (F) Duas partículas de cargas positivas e são fixadas nas extremidades de um bastão isolante de comprimento . Uma terceira partícula carregada pode se mover livremente ao longo do comprimento do bastão.

(a) Em que posição ao longo do bastão a terceira partícula estará em equilíbrio?

1. (F) Duas partículas de cargas positivas e são fixadas nas extremidades de um bastão isolante de comprimento . Uma terceira partícula carregada pode se mover livremente ao longo do comprimento do bastão.

(b) Discuta a estabilidade do equilíbrio dessa partícula em função do sinal de sua carga. (Dica: considere pequenos deslocamentos a partir da posição de equilíbrio)

3. (F) Duas partículas idênticas de carga são fixadas sobre o eixo de um sistema de coordendas, como mostrado na figura abaixo. Cada uma encontra-se a uma distância da origem. Uma terceira partícula de carga encontra-se sobre o eixo , a uma distância da origem, e pode se mover livremente sobre este eixo.

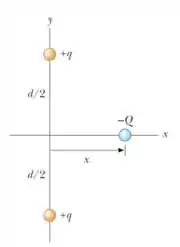
(a) Determine o vetor força resultante sobre a partícula de carga .

3. (F) Duas partículas idênticas de carga são fixadas sobre o eixo de um sistema de coordendas, como mostrado na figura abaixo. Cada uma encontra-se a uma distância da origem. Uma terceira partícula de carga encontra-se sobre o eixo , a uma distância da origem, e pode se mover livremente sobre este eixo.

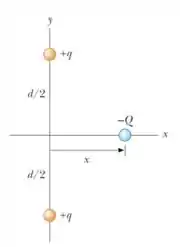
(b) Suponha que a partícula de carga é abandonada do repouso em um ponto . Descreva qualitativamente o movimento dessa partícula. O que acontece quando ela ultrapassa a origem?

5. Em um modelo clássico para o átomo de Hidrogênio, um elétron de carga e massa descreve um movimento circular uniforme de raio em torno de um próton de carga , fixo na origem. Considerando a força de atração gravitacional entre o próton e o elétron desprezível em confronto com a força elétrica, determine:

(a) A aceleração do elétron (módulo, direção e sentido).

5. (M) Em um modelo clássico para o átomo de Hidrogênio, um elétron de carga e massa descreve um movimento circular uniforme de raio em torno de um próton de carga , fixo na origem. Considerando a força de atração gravitacional entre o próton e o elétron desprezível em confronto com a força elétrica, determine:

(b) A velocidade escalar do elétron.

5. (M) Em um modelo clássico para o átomo de Hidrogênio, um elétron de carga e massa descreve um movimento circular uniforme de raio em torno de um próton de carga , fixo na origem. Considerando a força de atração gravitacional entre o próton e o elétron desprezível em confronto com a força elétrica, determine:

(c) O período de revolução.

5. (M) Em um modelo clássico para o átomo de Hidrogênio, um elétron de carga e massa descreve um movimento circular uniforme de raio em torno de um próton de carga , fixo na origem. Considerando a força de atração gravitacional entre o próton e o elétron desprezível em confronto com a força elétrica, determine:

(d) Por que podemos desprezar a força gravitacional nessa situação?

6. (M) Uma partícula de massa e carga penetra na região entre as placas metálicas de um capacitor, como indicado na figura abaixo. As placas estão separadas por uma distância e produzem um campo elétrico uniforme em seu interior. Ao entrar nessa região, a partícula possui uma velocidade inicial paralela às placas e está a uma mesma distância delas. Considere ainda que os efeitos da força gravitacional são desprezíveis em confronto com os da força elétrica. Utilizando o sistema de coordenadas indicado na figura, determine:

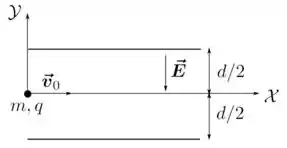
(a) O vetor aceleração da partícula.

6. (M) Uma partícula de massa e carga penetra na região entre as placas metálicas de um capacitor, como indicado na figura abaixo. As placas estão separadas por uma distância e produzem um campo elétrico uniforme em seu interior. Ao entrar nessa região, a partícula possui uma velocidade inicial paralela às placas e está a uma mesma distância delas. Considere ainda que os efeitos da força gravitacional são desprezíveis em confronto com os da força elétrica. Utilizando o sistema de coordenadas indicado na figura, determine:

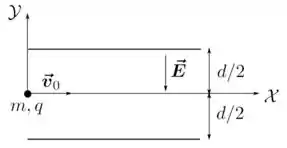
(b) O vetor velocidade da partícula como função do tempo .

6. (M) Uma partícula de massa e carga penetra na região entre as placas metálicas de um capacitor, como indicado na figura abaixo. As placas estão separadas por uma distância e produzem um campo elétrico uniforme em seu interior. Ao entrar nessa região, a partícula possui uma velocidade inicial paralela às placas e está a uma mesma distância delas. Considere ainda que os efeitos da força gravitacional são desprezíveis em confronto com os da força elétrica. Utilizando o sistema de coordenadas indicado na figura, determine:

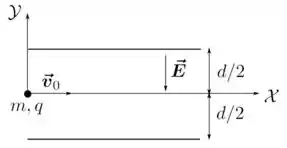
(c) O vetor posição da partícula como função do tempo .

6. (M) Uma partícula de massa e carga penetra na região entre as placas metálicas de um capacitor, como indicado na figura abaixo. As placas estão separadas por uma distância e produzem um campo elétrico uniforme em seu interior. Ao entrar nessa região, a partícula possui uma velocidade inicial paralela às placas e está a uma mesma distância delas. Considere ainda que os efeitos da força gravitacional são desprezíveis em confronto com os da força elétrica. Utilizando o sistema de coordenadas indicado na figura, determine:

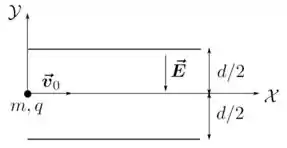
(d) A equação da trajetória, isto é, como função de . Que curva corresponde a essa equação?

6. (M) Uma partícula de massa e carga penetra na região entre as placas metálicas de um capacitor, como indicado na figura abaixo. As placas estão separadas por uma distância e produzem um campo elétrico uniforme em seu interior. Ao entrar nessa região, a partícula possui uma velocidade inicial paralela às placas e está a uma mesma distância delas. Considere ainda que os efeitos da força gravitacional são desprezíveis em confronto com os da força elétrica. Utilizando o sistema de coordenadas indicado na figura, determine:

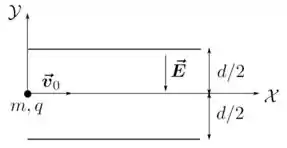
(e) O vetor velocidade da partícula ao sair da região das placas, supondo que elas possuem um comprimento . Qual será a sua deflexão, isto é, o ângulo que este vetor faz com a horizontal?

7. (D) Uma barra isolante e fina de comprimento é posicionada sobre o eixo de um sistema de coordenadas, de modo que suas extremidades estão em . Ela possui uma carga total uniformemente distribuída sobre seu comprimento.

(a) Determine o campo elétrico (módulo, direção e sentido) produzido pela barra em um ponto sobre o eixo , localizado a uma distância da origem.

9. (D) Um fio semicircular fino, de raio , encontra-se no plano , com seu centro na origem de um sistema de coordenadas cartesianas e contido nos primeiro e segundo quadrantes, como mostrado na figura abaixo. Ele possui uma densidade linear de carga elétrica constante e positiva

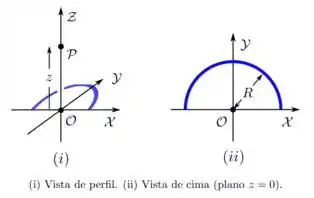
(a) Qual(is) componente(s) do vetor campo elétrico resultante em um ponto qualquer do eixo é(são) nula(s)? Justifique.

9. (D) Um fio semicircular fino, de raio , encontra-se no plano , com seu centro na origem de um sistema de coordenadas cartesianas e contido nos primeiro e segundo quadrantes, como mostrado na figura abaixo. Ele possui uma densidade linear de carga elétrica constante e positiva

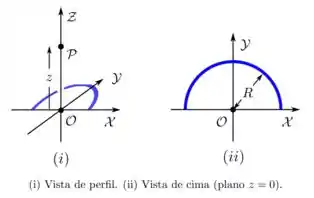
(b) Deduza, em detalhe, uma expressão para o vetor campo elétrico resultante no ponto acima mencionado.

9. (D) Um fio semicircular fino, de raio , encontra-se no plano , com seu centro na origem de um sistema de coordenadas cartesianas e contido nos primeiro e segundo quadrantes, como mostrado na figura abaixo. Ele possui uma densidade linear de carga elétrica constante e positiva

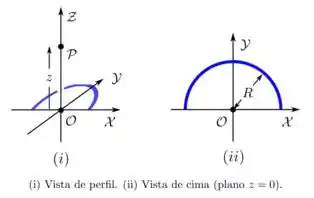
(c) Obtenha uma expressão assintótica para o resultado do item anterior no limite em que o ponto está muito distante do fio, de forma que . Discuta o resultado.

12. (M) Considere o dipolo elétrico mostrado na figura abaixo.

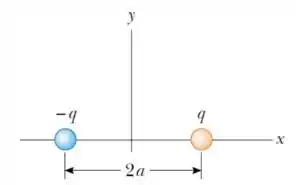
(a) Determine o vetor campo elétrico produzido pelo dipolo em um ponto sobre o eixo , localizado a uma distância da origem.

12. (M) Considere o dipolo elétrico mostrado na figura abaixo.

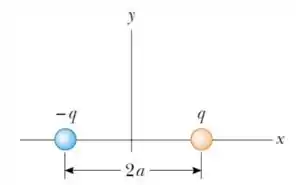
(b) Determine o vetor campo elétrico produzido pelo dipolo em um ponto sobre o eixo , localizado a uma distância da origem.

12. (M) Considere o dipolo elétrico mostrado na figura abaixo.

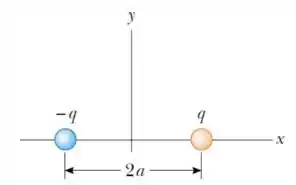
(c) Obtenha expressões assintóticas para os dois resultados acima nos limites e . Interprete os resultados.

11. (D) Uma casca isolante cilíndrica de raio e altura possui uma carga uniformemente distribuída sobre sua área.

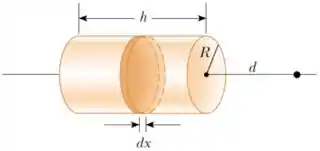
(a) Determine a densidade superficial de carga do cilindro.

Um disco circular isolante e fino, de raio , tem uma densidade superficial, de raio , tem uma densidade superficial de carga dada por , onde é uma constante positiva e é a distância ao centro do disco.

1. Determine a carga total contida no disco.

Um disco circular isolante e fino, de raio , tem uma densidade superficial, de raio , tem uma densidade superficial de carga dada por , onde é uma constante positiva e é a distância ao centro do disco.

1. Determine o vetor campo elétrico em um ponto localizado sobre o eixo perpendicular ao plano do disco e que passa pelo seu centro, a uma distância do mesmo.

Sugestão: divida o disco em aneis infinitesimais concêntricos e use o resultado obtido em aula para o campo elétrico produzido por um anel uniformemente carregado (por que podemos fazer isto?).

Um disco circular isolante e fino, de raio , tem uma densidade superficial, de raio , tem uma densidade superficial de carga dada por , onde é uma constante positiva e é a distância ao centro do disco.

1. Considere agora que este ponto está muito longe do disco, de forma que . Determine uma expressão assintótica para o resultado do item anterior neste limite e interprete o resultado.

11. (D) Uma casca isolante cilíndrica de raio e altura possui uma carga uniformemente distribuída sobre sua área.

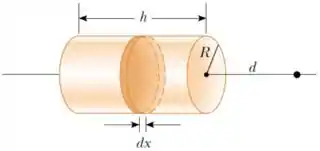
(b) Determine o vetor campo elétrico a uma distância do lado direito do cilindro, como indicado na figura. Sugestão: Divida o cilindro em anéis infinitesimais coaxiais como indicado na figura e use o resultado obtido em aula para o campo elétrico produzido por um anel uniformemente carregado. A integral resultante pode ser resolvida por substituição simples.

11. (D) Uma casca isolante cilíndrica de raio e altura possui uma carga uniformemente distribuída sobre sua área.

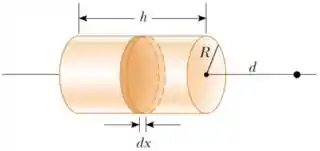
(c) Discuta o comportamento da expressão obtida no item anterior no limite .

13. Três cargas puntiformes , e são posicionadas ao longo do eixo de um sistema de coordenadas, como indicado na figura abaixo. A separação entre duas cargas adjacentes vale .

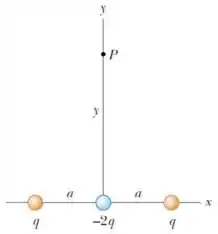
(b) Obtenha uma expressão assintótica para o resultado acima no limite , ou seja, quando está muito distante das cargas. Compare o seu resultado com os casos de um monopolo e de um dipolo elétrico e discuta as diferenças.

13. Três cargas puntiformes , e são posicionadas ao longo do eixo de um sistema de coordenadas, como indicado na figura abaixo. A separação entre duas cargas adjacentes vale .

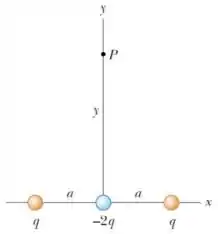
(c) Utilizando o princípio da superposição, discuta como essa distribuição de cargas pode ser entendida como uma composição de dipolos elétricos. Qual é a intensidade do momento de dipolo elétrico total desta distribuição?

Uma barra isolante e fina de comprimento 2a é posicionada sobre o eixo X de um sistema de coordenadas, de modo que suas extremidades estão em . Ela possui uma carga total Q uniformemente distribuída sobre seu comprimento. Uma segunda barra, idêntica à primeira e com a mesma carga total Q uniformemente distribuída sobre seu comprimento, é posicionada sobre o eixo X com suas extremidades em . Determine a força elétrica (módulo, direção e sentido) que a primeira barra exerce sobre a segunda. Sugestão: Divida a segunda barra em elementos infinitesimais de carga e considere a interação entre estes elementos e a primeira barra.