UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 1 - Carga Elétrica e Campo Elétrico, Questão 3b
3. (F) Duas partículas idênticas de carga são fixadas sobre o eixo de um sistema de coordendas, como mostrado na figura abaixo. Cada uma encontra-se a uma distância da origem. Uma terceira partícula de carga encontra-se sobre o eixo , a uma distância da origem, e pode se mover livremente sobre este eixo.
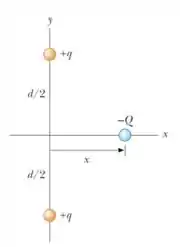
(b) Suponha que a partícula de carga é abandonada do repouso em um ponto . Descreva qualitativamente o movimento dessa partícula. O que acontece quando ela ultrapassa a origem?
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema temos duas cargas no eixo a uma distância da origem e uma terceira carga está no eixo a uma distância da origem. Nessa situação queremos saber como a carga se comporta ao ser solta a partir de uma posição e o que acontece quando a carga passa pela origem.
Tem ideia de como fazer isso? 😬
Anteriormente calculamos a força resultante na carga como
O podemos tirar dessa equação? 👀
Passo 2
Fazendo , temos
Perceba que o termo é positivo quando a carga está sob o semieixo positivo de pois será maior que . Dessa forma, a força resultante aponta para , fazendo a carga ir em direção a origem.
Mas quando a carga passa para o lado negativo, o termo fica negativo e consequentemente a força resultante aponta para , fazendo a carga desacelerar e voltar para o semieixo positivo de .
Portanto a carga admite um movimento cíclico andando de para .
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
