UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 1 - Carga Elétrica e Campo Elétrico, Questão 6c
6. (M) Uma partícula de massa e carga penetra na região entre as placas metálicas de um capacitor, como indicado na figura abaixo. As placas estão separadas por uma distância e produzem um campo elétrico uniforme em seu interior. Ao entrar nessa região, a partícula possui uma velocidade inicial paralela às placas e está a uma mesma distância delas. Considere ainda que os efeitos da força gravitacional são desprezíveis em confronto com os da força elétrica. Utilizando o sistema de coordenadas indicado na figura, determine:
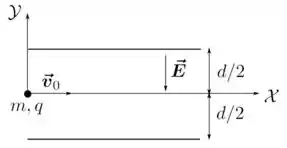
(c) O vetor posição da partícula como função do tempo .
Passo 1
E aí! Suave na nave?! Tá difícil essa questão? Relaxa que a gente vai te ajudar!
Nesse problema temos uma partícula de massa , carga e velocidade inicial (horizontal) e então essa partícula entra em uma região entre duas placas de um capacitor, a uma distância de cada uma, que possui um campo em seu interior que aponta para baixo.
Nessa condição, queremos obter o vetor posição da partícula ao entrar na região.
Tem alguma ideia do que fazer? 😐
Se lembrarmos lá de física 1, lembramos que a partir da integral da equação da velocidade, podemos obter a equação da posição.
Aqui podemos aplicar a mesma coisa.
Anteriormente vimos que o vetor velocidade da partícula á dada por
Assim, integrando esse resultado em relação a , obtemos o vetor posição...
Sacou? Bora começar! 😉
Passo 2
De maneira mais matemática, o que vamos fazer é
Substituindo o vetor
Pelo método de integração polinomial, chegamos em
e surgiram a partir das constantes de integração. Mas como consideramos que a partícula partiu da origem do sistema, então
O que achou? Foi de boa? Responde aí! 😊
