UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 1 - Carga Elétrica e Campo Elétrico, Questão 1a
1. (F) Duas partículas de cargas positivas e são fixadas nas extremidades de um bastão isolante de comprimento . Uma terceira partícula carregada pode se mover livremente ao longo do comprimento do bastão.
(a) Em que posição ao longo do bastão a terceira partícula estará em equilíbrio?
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nesse problema temos duas cargas, cada uma em uma extremidade de uma barra de comprimento . Uma carga possui carga e outra possui carga . Uma terceira carga é colocada sobre a barra e ela é capaz de se mover livremente.
Nesse esquema queremos saber qual é a posição da terceira barra que faça ela entrar em equilíbrio.
Tem alguma ideia do que fazer? 😉
Para a terceira carga entrar em equilíbrio, a força entre a carga e as cargas e tem que ser iguais.
A força entre duas cargas é dada por
Com .
Bora começar? 👀
Passo 2
Desenhando o problema, temos
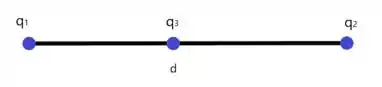
Calculando a força de pra , temos
Como
Agora fazendo a equação da força de para
Como
Para estar em equilíbrio, tem que ser igual a
Tranquilo até aqui? 😎
Passo 3
Se a barra tem comprimento , podemos dizer que a distância entre e é e consequentemente a distância entre e é , ou seja, e
Tirando a raiz nos dois lados para eliminar o expoente ...
Portanto, deve estar a da carga .
Fim! Iae, o que achou? Responde Aí! 😁
Resposta
deve estar a da carga