Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campo Elétrico Gerado por uma Carga Pontual

Ver Teoria
Exercício 7712345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576787980818283848586878889909192

Enunciado

UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 1 - Carga Elétrica e Campo Elétrico, Questão 3a

3. (F) Duas partículas idênticas de carga q > 0 são fixadas sobre o eixo Y de um sistema de coordendas, como mostrado na figura abaixo. Cada uma encontra-se a uma distância d / 2 da origem. Uma terceira partícula de carga - Q   ( Q > 0 ) encontra-se sobre o eixo X , a uma distância x da origem, e pode se mover livremente sobre este eixo.

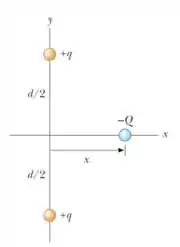
(a) Determine o vetor força resultante sobre a partícula de carga - Q .

Passo 1

Iae! Como vai, meu querido? 😁 Bora aprender mais uma questão? 😉

Nesse problema temos duas cargas q no eixo y a uma distância d / 2 da origem e uma terceira carga - Q está no eixo x a uma distância x da origem. Nessa situação queremos saber qual a força resultante na carga - Q .

Tem ideia de como fazer isso? 😬

A força entre duas cargas é calculada a partir da fórmula

F = k q 1 q 2 r 2

Como temos duas cargas fixas, a força F resultante é dada pela soma das forças em - Q .

Sacou? Bora começar! 😁

Passo 2

Calculando a força entre - Q e a carga q que está no semieixo positivo de y .

F 12 → = k q - Q x 2 + d 2 2 cos ⁡ θ i + k q - Q x 2 + d 2 2 sin ⁡ θ j

F 12 → = - q Q k 1 x 2 + d 2 4 cos ⁡ θ i + 1 x 2 + d 2 4 sin ⁡ θ j

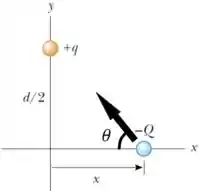
Tranquilo até aqui? 😉

Passo 3

Agora vamos fazer o mesmo para a carga situada no semieixo negativo de y

F 13 → = k q - Q x 2 + - d 2 2 cos ⁡ θ i - k q - Q x 2 + - d 2 2 sin ⁡ θ j

F 13 → = - q Q k 1 x 2 + d 2 4 cos ⁡ θ i - 1 x 2 + d 2 4 sin ⁡ θ j

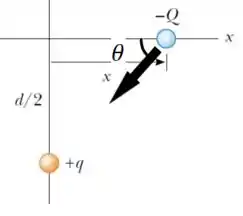
Bacana, não é? 😁

Passo 4

Somando as forças F 12 → e F 13 → , temos que a força resultante é dada por

F R → = F 12 → + F 13 →

F R → = - q Q k 1 x 2 + d 2 4 cos ⁡ θ i + 1 x 2 + d 2 4 sin ⁡ θ j + - q Q k 1 x 2 + d 2 4 cos ⁡ θ i - 1 x 2 + d 2 4 sin ⁡ θ j

F R → = - q Q k 1 x 2 + d 2 4 cos ⁡ θ i + 1 x 2 + d 2 4 sin ⁡ θ j + 1 x 2 + d 2 4 cos ⁡ θ i - 1 x 2 + d 2 4 sin ⁡ θ j

F R → = - q Q k 2 x 2 + d 2 4 cos ⁡ θ i

Pegou o esquema? Responde Aí! 😁

Resposta

F R → = - q Q k 2 x 2 + d 2 4 cos ⁡ θ i

Exercícios de Livros Relacionados

Duas cargas puntiformes, q 1 = 2,0p C e q 2 = - 2,0p C são separadas por 4,0μ m . (a) Qual é o módulo de dipolo deste par de cargas? (b) Represente o par e mostre a direção e o sentido do momento de d
Um elétron que tem uma energia cinética igual a 2,00 × 10 - 16J está se movendo para a direita ao longo do eixo de um tubo de raios catódicos, como mostra a Figura 21-40. Um campo elétrico E → = 2,00
Um elétron é liberado a partir do repouso em um campo elétrico pouco intenso dado por E → = - 1,50 × 10 - 10N / Cy ^ . Depois que o elétron percorre uma distância vertical de 1,0μ m , qual o valor do
Qual é o campo elétrico de um núcleo de Ferro a uma distância igual a 6,00x10 - 10m do núcleo? O número atômico do ferro é igual a 26. Suponha que o núcleo possa ser considerado uma carga puntiforme.
Uma carga puntiforme de +8,75μ C está colada em uma mesa horizontal com atrito desprezível. Ela está atada a uma carga puntiforme de -6,5μ C por um por um fio leve, não condutor, de 2,5c m . Um campo