UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 1 - Carga Elétrica e Campo Elétrico, Questão 9a
9. (D) Um fio semicircular fino, de raio , encontra-se no plano , com seu centro na origem de um sistema de coordenadas cartesianas e contido nos primeiro e segundo quadrantes, como mostrado na figura abaixo. Ele possui uma densidade linear de carga elétrica constante e positiva
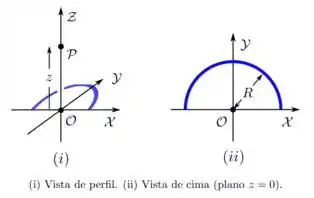
(a) Qual(is) componente(s) do vetor campo elétrico resultante em um ponto qualquer do eixo é(são) nula(s)? Justifique.
Passo 1
Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema temos uma linha de carga em forma de semicircunferência situada no plano e em . Essa linha de carga possui um raio da origem do sistema e uma densidade linear de carga positiva.
Dessa forma, queremos responder a seguinte pergunta: para qual componente vetorial o vetor campo elétrico é sempre nulo?
Tem ideia de como fazer isso? 😬
O vetor campo elétrico gerado a partir de uma carga é dado por
Ou seja, para uma componente ser nulo, o versor deve ser nulo em algum componente.
O valor de da linha de carga é arbitrário, então para essa análise podemos atribuir um valor a ela e fazer a análise do vetor para dois casos: primeiro no plano e depois quando .
Tranquilo até aqui? 😉
Passo 2
No plano , temos
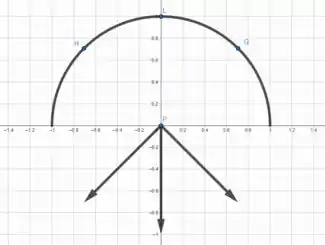
Perceba que nesse caso, para cada pedaço infinitesimal da distribuição de carga há uma simetria no eixo que faz com que tenha uma contribuição tanto em quanto que se opõe à componente do vetor resultante.
Por exemplo, no nosso caso, temos uma contribuição do pedaço que gera um vetor genérico e um outro pedaço que gera uma contribuição
Assim, como a distribuição de cargas é uniforme, então , dessa forma somando o vetor resultante , as componentes em sempre se cancelam.
Bacana, não é? 😁
Passo 3
Agora se fizermos o ponto subir um pouco em , onde .
Podemos afirmar que visto de cima, o vetor resultante não muda, então em , continua nulo.
A partir de uma vista lateral, temos a seguinte visão
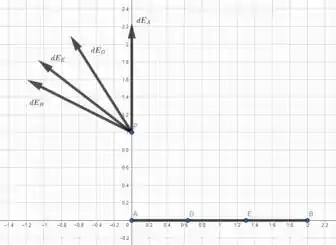
Assim, vemos que em o vetor resultante não é nulo pois não há uma simetria que faça as componentes se cancelarem
Logo, apenas no eixo o campo elétrico é nulo.
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
Em o vetor resultante é nulo.