Duas esferas idênticas, cada uma com massa , são suspensas por fios ideais e isolantes de comprimento , como indicado na figura abaixo. Elas possuem cargas de mesmo módulo e sinais opostos e estão sob a ação de um campo elétrico uniforme , de direção horizontal e intensidade desconhecida, e do campo gravitacional . Quando o sistema está em equilíbrio, o ângulo que os fios fazem com a vertical vale . Nessas condições, determine:
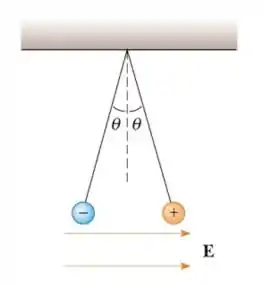
- A tensão no fio
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá esferas com cargas iguais e opostas em sinal suspensas por fios ideais e isolantes, e que estão sob ação de um campo elétrico .
Sabendo disso, a questão nos pede para calcularmos a tensão no fio.
Já vou dizendo logo que, pela simetria do sistema, a tração em ambos os fios é igual!
Dessa forma, devemos aplicar o diagrama de corpo livre para uma das esferas e analisar as forças.
Dessa forma, basta aplicarmos a Lei de Newton!!
E aí? Bora lá??!!
😉
Passo 2
Assim, sabemos que cada esfera tem massa . Logo, fazendo o diagrama de corpo livre da esfera de carga positiva, temos:
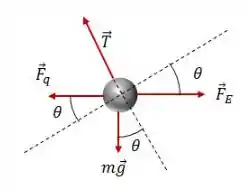
Onde é a tração no fio, é a força gerada pelo campo elétrico, é a força de atração entre as cargas, é a aceleração da gravidade e é o ângulo entre o fio e o eixo vertical.
Dessa forma, aplicando a Lei de Newton para as forças na direção da tração, temos:
Agora, precisamos descobrir quem é e para substituir nessa fórmula!
Passo 3
Para descobrir , sabemos que a força elétrica entre duas cargas é dada da seguinte forma:
Onde é a constante eletrostática e é a distância entre as cargas e .
Dessa forma, aplicando na nossa questão, temos:
Considerando que , onde é o comprimento do fio, temos:
Por outro lado, a força gerada pelo campo elétrico depende apenas da carga positiva. E esta força é dada da seguinte forma:
Passo 4
Dessa forma, substituindo e na equação do Passo 2, temos:
Entendeu direitinho? Responde aee ;)
