UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 1 - Carga Elétrica e Campo Elétrico, Questão 11b
11. (D) Uma casca isolante cilíndrica de raio e altura possui uma carga uniformemente distribuída sobre sua área.
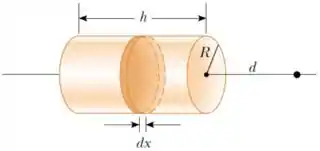
(b) Determine o vetor campo elétrico a uma distância do lado direito do cilindro, como indicado na figura. Sugestão: Divida o cilindro em anéis infinitesimais coaxiais como indicado na figura e use o resultado obtido em aula para o campo elétrico produzido por um anel uniformemente carregado. A integral resultante pode ser resolvida por substituição simples.
Passo 1
Iae! Como vai, meu querido? 😁 Bora aprender mais uma questão? 😉
Nessa questão temos uma casca cilíndrica com raio , comprimento e carga que é distribuída uniformemente.
Com isso, queremos determinar o vetor campo elétrico a uma distância da casca cilíndrica.
Tem ideia de como fazer isso? 👀
O campo elétrico de uma carga é dado pela equação
Manipulando essa equação para discos infinitesimais, vamos chegar em uma integral dupla .
Sacou? Bora começar! 😉
Passo 2
Vamos começar reescrevendo ...
Pela figura do enunciado, vemos que , e formam um triangulo retângulo com sendo a hipotenusa, portanto podemos reescrever em função de e , com representando o eixo como
Substituindo em , temos
Para cada ponto infinitesimal de um disco infinitesimal da superfície, temos uma contribuição
Anteriormente calculamos a densidade superficial de cargas como
E se , então
Substituindo em sabendo que ...
Para cada valor de temos um valor
Tranquilo até aqui? 😬
Passo 3
Integrando nos dois lados da igualdade, chegamos em
varia de a e de a , como vemos na figura do enunciado
Como não temos para integrar, então
Aplicando o método de substituição, vamos chegar em
Aplicando os limites de integração...
Assim, substituindo em
Pegou o esquema? Responde Aí! 😁
