UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 1 - Carga Elétrica e Campo Elétrico, Questão 7a
7. (D) Uma barra isolante e fina de comprimento é posicionada sobre o eixo de um sistema de coordenadas, de modo que suas extremidades estão em . Ela possui uma carga total uniformemente distribuída sobre seu comprimento.
(a) Determine o campo elétrico (módulo, direção e sentido) produzido pela barra em um ponto sobre o eixo , localizado a uma distância da origem.
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema temos uma barra com densidade de carga constante, de comprimento , carga total e sob o eixo . A partir dessa descrição, temos que obter o campo elétrico em um ponto sobre o eixo situado a .
Desenhando o problema, temos
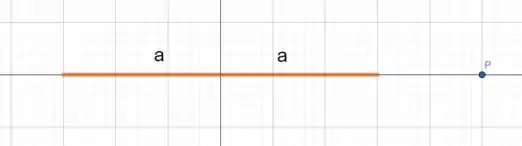
Para resolver esse problema, vamos dividir o comprimento da barra em tamanhos infinitesimais . Assim, se o campo elétrico a partir de uma carga é dada por
Para cada valor infinitesimal da barra, temos uma contribuição a partir de uma carga , ou seja
A partir daqui podemos resolver essa equação e encontrar um valor para o campo elétrico no ponto .
Bora lá! 😉
Passo 2
Foi dito que a densidade linear de carga da barra é constante, ou seja
Substituindo na equação fazendo , temos
Integrando nos dois lados da igualdade, chegamos em
Considerando que o ponto está a uma distância da barra, podemos integrar de até , ou seja
Tranquilo até aqui? 😁
Passo 3
Integrando , chegamos em
Podemos escrever a densidade linear de cargas da barra como
Substituindo em
O campo elétrico aponta na direção de , ou seja, em
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
