UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 1 - Carga Elétrica e Campo Elétrico, Questão 9b
9. (D) Um fio semicircular fino, de raio , encontra-se no plano , com seu centro na origem de um sistema de coordenadas cartesianas e contido nos primeiro e segundo quadrantes, como mostrado na figura abaixo. Ele possui uma densidade linear de carga elétrica constante e positiva
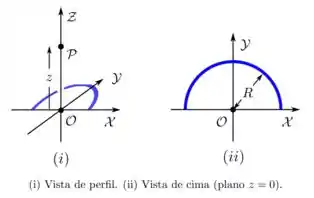
(b) Deduza, em detalhe, uma expressão para o vetor campo elétrico resultante no ponto acima mencionado.
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nesse problema temos uma linha de carga em forma de semicircunferência situada no plano e em . Essa linha de carga possui um raio da origem do sistema e uma densidade linear de carga positiva.
Dessa forma, queremos obter o vetor campo elétrico no ponto
Tem ideia de como fazer isso? 😬
Dado o vetor
Já sabemos que a componente do vetor é nulo, ou seja, .
Agora para obter as componentes e temos que fazer uma análise dos vetores de cada contribuição infinitesimal do arco.
Para , temos que o vetor formado possui um ângulo em relação a , que vamos chamar de , e outro ângulo em relação a , que vamos chamar de , assim, podemos escrever :
Já para vamos ter:
Tranquilo até aqui? 👀
Passo 2
Vamos obter o vetor resultante em primeiro:
Se , então para cada contribuição da linha de carga temos:
E pela lei dos senos, temos:
Substituindo em :
Fazendo :
Substituindo por uma variação do ângulo e substituindo em , temos:
Integrando nos dois lados:
O ângulo que faz com varia de a , portanto é o valor que temos que substituir na integral:
Por último, temos :
Complicado, né? 👀
Passo 3
Agora vamos obter a componente do vetor campo elétrico:
Substituindo novamente e dessa vez fazendo pela lei dos cossenos, temos:
Substituindo :
Novamente vamos substituir por , assim como fazemos no passo anterior:
Integrando nos dois lados com variando entre e :
Queremos um resultado em função da carga total , ou seja, fazemos
E finalmente, obtemos o vetor campo elétrico dado por
Fim! Iae, o que achou? Responde Aí! 😁
