UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 1 - Carga Elétrica e Campo Elétrico, Questão 13b
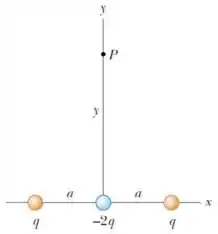
13. Três cargas puntiformes , e são posicionadas ao longo do eixo de um sistema de coordenadas, como indicado na figura abaixo. A separação entre duas cargas adjacentes vale .
(b) Obtenha uma expressão assintótica para o resultado acima no limite , ou seja, quando está muito distante das cargas. Compare o seu resultado com os casos de um monopolo e de um dipolo elétrico e discuta as diferenças.
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema temos três cargas distribuídas no eixo de um sistema cartesiano onde em e em temos cada um uma carga e na origem do sistema temos uma carga .
A partir daí, queremos saber qual é o valor do campo elétrico em um ponto em que .
Tem alguma ideia de como fazer isso? 🤔
Anteriormente calculamos o campo elétrico como
A partir dessa equação, vamos considerar e verificar como se comporta...
Sacou? Bora começar! 😉
Passo 2
Perceba que no denominador, temos , assim, se , então .
Substituindo essa aproximação em , vamos obter
Perceba que o resultado resultou em pelo fato de haver uma simetria no eixo tanto fisicamente na distribuição das cargas quanto no valor das cargas.
Assim, como , para o ponto temos um dipolo com cargas de mesmo módulo em que uma carga anula a outra.
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
