UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 1 - Carga Elétrica e Campo Elétrico, Questão 4c
Três cargas puntiformes − e são posicionadas sobre os vértices de um triângulo equilátero de lado a, como indicado na figura abaixo.
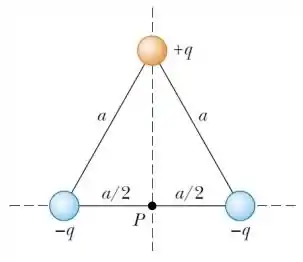
(c) Determine o vetor força elétrica resultante sobre uma das cargas .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para calcular a força elétrica resultante sobre uma das cargas .
Para isso, primeiro temos que analisar quais são as forças que agem sobre essa carga. Se liga na figura abaixo:
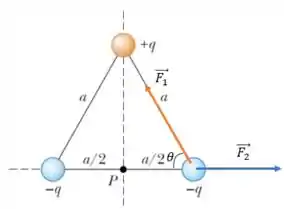
Lembrando que, pela Lei de Coulomb, a força elétrica entre duas cargas é dada por:
Onde é a constante dielétrica do vácuo e é a distância entre as cargas e .
Agora temos que ver a força de cada uma e utilizar o teorema da superposição para encontrarmos a força resultante:
Obs: como sabemos que se trata de um triângulo equilátero, vemos que:
E aí? Bora lá??!!
😉
Passo 2
Assim, para o módulo de , temos:
Aplicando a componente vertical de :
E para a componente horizontal de :
Logo, temos o vetor
Passo 3
Por outro lado, para , temos:
Como só há componente horizontal e na direção positiva do eixo , então temos que:
Passo 4
Assim, pelo Teorema da Superposição, temos:
Entendeu direitinho? Responde aee ;)
