UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 1 - Carga Elétrica e Campo Elétrico, Questão 12c
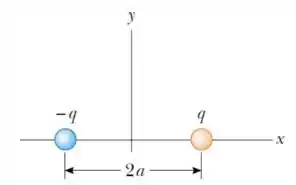
12. (M) Considere o dipolo elétrico mostrado na figura abaixo.
(c) Obtenha expressões assintóticas para os dois resultados acima nos limites e . Interprete os resultados.
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema temos um dipolo formado por uma carga e outra carga igualmente espaçados em relação ao eixo .
Dessa forma, queremos obter a expressão que descreve os campos elétricos em um ponto em e em .
Tem ideia de como fazer isso? 🤔
Anteriormente vimos que o campo elétrico no caso 1 em que o ponto estava sob o eixo tínhamos
Já no caso 2, quando o ponto estava sob o eixo e o campo elétrico é dado por
Para auxiliar na nossa simplificação, foi dito que para , .
Bora começar! 😐
Passo 2
Vamos começar pelo caso 1...
Se , podemos aproximar como , ou seja
Além disso, fazendo
Tranquilo até aqui? 😉
Passo 3
Agora vamos analisar o caso
Nesse caso: para , , ou seja
Substituindo na equação
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
