UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 1 - Carga Elétrica e Campo Elétrico, Questão 4b
Três cargas puntiformes − e são posicionadas sobre os vértices de um triângulo equilátero de lado a, como indicado na figura abaixo.
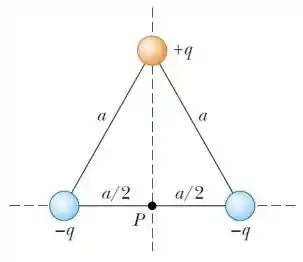
(b) Determine o vetor campo elétrico no centro do triângulo.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para calcular o vetor campo elétrico no ponto indicado na figura abaixo:
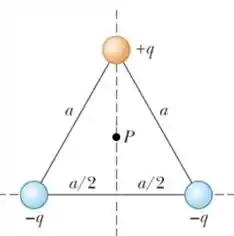
Para isso, temos que ver o campo elétrico individual de cada carga sobre o ponto .
Lembrando que o módulo do campo elétrico é dado por:
Onde é a constante dielétrica do vácuo e é a distância entre a carga e o ponto que queremos.
Se observarmos bem a figura, vemos que as duas cargas são simétricas e isso vai reduzir nossos cálculos hehe.
Quer saber como? Vamos junto aqui então!!
😉
Passo 2
Assim, primeiro vamos fazer o campo elétrico da carga sobre o ponto , ou seja, queremos descobrir :
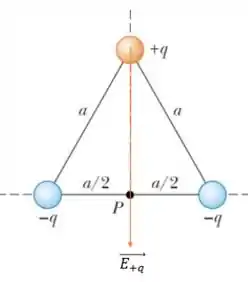
Assim, aplicando na equação do campo elétrico, temos (lembrando que a altura de um triângulo equilátero é ):
Como não há componentes horizontais e a componente vertical aponta para baixo, então o vetor é dado por:
Passo 3
Agora, para o campo elétrico das cargas sobre o ponto , percebemos que pela simetria as componentes irão se cancelar:
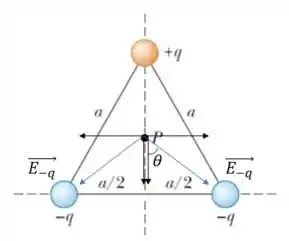
Assim, temos que:
Assim, para o campo , temos:
Assim, substituindo em , temos:
Como não há componentes horizontais e a componente vertical aponta para baixo, então o vetor é dado por:
Passo 4
Agora, aplicando o princípio da superposição, temos o campo resultante:
Entendeu direitinho? Responde aee ;)
