UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 1 - Carga Elétrica e Campo Elétrico, Questão 9c
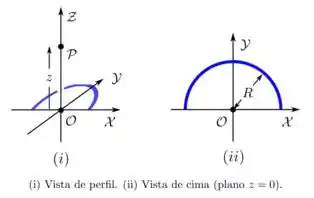
9. (D) Um fio semicircular fino, de raio , encontra-se no plano , com seu centro na origem de um sistema de coordenadas cartesianas e contido nos primeiro e segundo quadrantes, como mostrado na figura abaixo. Ele possui uma densidade linear de carga elétrica constante e positiva
(c) Obtenha uma expressão assintótica para o resultado do item anterior no limite em que o ponto está muito distante do fio, de forma que . Discuta o resultado.
Passo 1
Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉
Nesse problema temos uma linha de carga em forma de semicircunferência situada no plano e em . Essa linha de carga possui um raio da origem do sistema e uma densidade linear de carga positiva.
Dessa forma, queremos analisar o caso em que no ponto .
Tem ideia de como fazer isso? 😬
Anteriormente calculamos o vetor campo elétrico como
E nosso objetivo é analisar o que acontece com a expressão se .
Preparado? Bora lá! 😉
Passo 2
Se fizermos nas somas podemos simplificar que é igual a já que é dominante em relação a , ou seja
Fazendo essa simplificação na equação
Simplificando...
Na componente em temos , mas se então podemos dizer também que tende a
Dessa forma, o vetor resultante pode ser aproximado como
Ou seja, as dimensões da linha de carga não serão importantes e para o ponto , a linha de carga se comporta como uma carga pontual já que a equação é exatamente igual a equação do campo de uma carga pontual.
Sacou como faz? Responde Aí! 😉
