UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 1 - Carga Elétrica e Campo Elétrico, Questão 12b
12. (M) Considere o dipolo elétrico mostrado na figura abaixo.
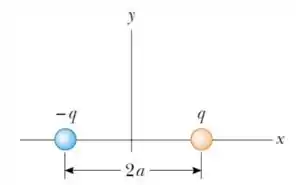
(b) Determine o vetor campo elétrico produzido pelo dipolo em um ponto sobre o eixo , localizado a uma distância da origem.
Passo 1
Iae! Como vai, meu querido? 😁 Bora aprender mais uma questão? 😉
Nesse problema temos um dipolo formado por uma carga e outra carga igualmente espaçados em relação ao eixo .
Dessa forma, queremos obter o vetor campo elétrico para um ponto situado sob o eixo com .
Tem ideia de como fazer isso? 🤔
Como temos duas cargas, o campo elétrico formado será obtido a partir da sobreposição dos campos gerados por cada carga.
Sacou? Bora começar! 😁
Passo 2
Vamos analisar a contribuição de cada carga separadamente.
Primeiro vamos analisar a carga .
Considerando que o ponto está a uma distância da carga , temos que a distância é dada por sendo que o versor aponta para , ou seja
Substituindo essas informações na equação do campo elétrico...
Agora para a carga , temos
Podemos perceber que novamente o versor aponta para e seu módulo agora possui .
Portanto a equação do campo para essa carga é dada por
Tranquilo até aqui? 😬
Passo 3
Dessa forma, o campo elétrico resultante nada mais é que a sobreposição dos campos de cada carga, ou seja, a soma de e
Simplificando a equação...
Pegou o esquema? Responde Aí! 😁
