Como construir e inverter uma TL e composição de TL’s
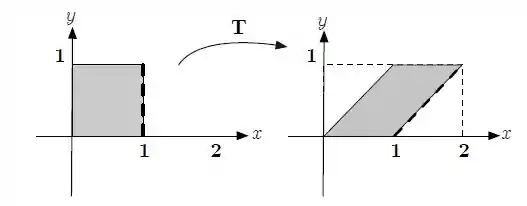
Considere a transformação linear definida pela figura abaixo:
Determine uma expressão para a imagem de um vetor
Determine onde e
Determine as matrizes de mudança de base de para e de para .
Passo 1
Letra
O que este item pede é a expressão analítica de , a sua fórmula. Pelas imagens vemos que o vértice do quadrado vira . E o vértice de baixo, , vira o vetor , ou seja, permanece igual. Assim podemos resumir em:
E assim, basta seguir o passo a passo de sempre.
Passo 2
Fazendo:
Como é linear:
Passo 3
Agora vamos achar valores para :
Substituindo:
Passo 4
Letra
Para começar construir a matriz , temos que aplicar nos vetores da base :
Passo 5
Agora vamos reescrever os vetores acima, nas coordenadas da base . Como é a base canônica, suas coordenadas na base , serão as próprias coordenadas do vetor. Assim:
E, portanto, nossa matriz fica:
Passo 6
Letra
Pera mas o que é uma matriz de mudança de base mesmo?
A matriz de mudança de base é simplesmente uma matriz que pega um vetor escrito nas coordenadas de uma base e leva ele para o mesmo vetor, só que escrito nas coordenadas de uma base .
E lembre-se também desse teorema!
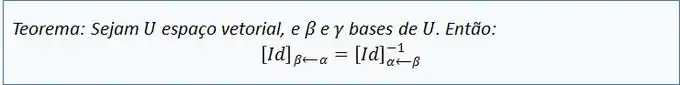
Agora, ficará mais fácil de resolver esta letra.
Passo 7
Vamos montar primeiro .
Como a transformação identidade transforma no próprio vetor, então ao aplicarmos nos vetores da base , dará os próprios vetores da base .
Assim, só temos que reescrevê-los na base . A escolha de fazer primeiro de para é mais fácil, pois não vamos fazer conta alguma, já que quando formos reescrever na base (que é a canônica), não precisaremos calcular nada! Assim:
Passo 8
E escrevendo nas coordenadas da base :
E, assim:
Passo 9
Agora é só inverter a matriz, pois, de acordo com o teorema láa em cima, e então
E assim:
Resposta
;