UFABC – Cálculo 1 – Lista 6 – 9a
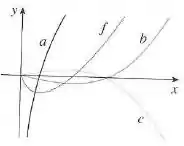
O gráfico de uma função está mostrado. Qual gráfico é uma primitiva de e por quê?
Passo 1
Bom galera, nesse exercício queremos encontrar o gráfico da antiderivada da função no gráfico apresentado. Para isso, iremos utilizar os conceitos de derivada conhecidos.
Passo 2
Olhando para o gráfico, podemos ver que para pequenos valores de em a nossa função é negativa. Dessa forma, o gráfico da antiderivada deve estar decrescendo. Para os demais valores, a nossa função é positiva, então a nossa função antiderivada deverá crescer nesses valores.
Passo 3
Olhando para o gráfico, podemos ver que a única função que satisfaz as condições é a função . Quando é negativa, está decrescendo, enquanto e estão crescendo. Quando é positiva, está crescendo. Dessa forma, a antiderivada da função é a curva .
Resposta
Olhando para o gráfico, podemos ver que a única função que satisfaz as condições é a função . Quando é negativa, está decrescendo, enquanto e estão crescendo. Quando é positiva, está crescendo. Dessa forma, a antiderivada da função é a curva .