UFSC – Cálculo 1 – Lista 4.2 – Questão 4a
Utilize os exercícios 1,2 e 3 da lista de exercícios 2.9 complementar para encontrar uma primitiva para as funções abaixo
Passo 1
E aí pessoal, tudo bem?
E o problema também deu uma dica: olhar a lista 2.9 (que fala sobre derivada de funções inversas, mais especificamente nos exercícios 1,2 e 3 da parte complementar). Mas por que olhar uma lista de derivadas? Porque uma primitiva é uma função cuja derivada é a função que temos.
Então a pergunta que precisamos nos fazer para achar a primitiva de é: qual é a função que derivando vai dar o arco seno??
E também precisamos relembrar o conceito de : é uma família de funções cuja derivada é a mesma! Como derivada de constante é zero, ao trocarmos de constante trocamos de primitiva, mas não de derivada!
Então o problema pede ara encontrarmos uma primitiva de .
Mas relaxa, vou fazer passo a passo com você!
Obs.: (vamos chamar de a primitiva de )
Passo 2
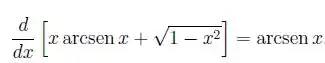Da lista que o professor fala, no exercício 1 temos que verificar a seguinte igualdade:
E se você for lá na lista 2.9 e verificar a resolução dela, vai ver que essa igualdade está correta!
Então respondendo nossa pergunta do passo 1: a função primitiva cuja derivada é o arco seno é
e as outras primitivas? Basta adicionar o no final! (derivada de constante é zero, por isso a troca não influencia na derivada)
Queremos uma primitiva apenas, então por simplicidade, podemos dizer que :
E é isso!
Beleza?
Espero ter ajudado! Vamos para a próxima?