Uma máquina do tipo caça-níqueis é composta por três discos que giram de forma independente, cada qual contendo as seguintes figuras: 2 laranjas, 3 bananas, 4 maçãs e 5 morangos. O apostador deve pagar 50 reais para jogar. Se sair 3 laranjas, ele ganha 250 reais; se sair 3 bananas, ganha 200 reais; se sair 3 maçãs, ganha 150 reais e se sair 3 morangos, ganha 100 reais; em qualquer outra situação ele perde. Pergunta-se: qual o lucro esperado de um jogador em uma jogada? E se o jogador fizer dez jogadas?
Passo 1
Tá, primeiro a gente tem que avaliar quais são as possibilidades de lucro que a gente tem.
E depois a gente calcula a probabilidade de cada uma acontecer, pra gente conhecer o lucro esperado.
Passo 2
Quais são os possíveis lucros ?
A gente sabe que independente do que sair, ele paga 50 reais.
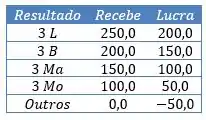
Bom, quando sair 3 laranjas, ele recebe 250 reais, tendo um lucro de 200 reais. Concorda?
Pensando da mesma forma:
Qualquer outro resultado que saia ele tem um prejuízo de 50 reais. Beleza?
Passo 3
Organizando numa tabela pra ficar mais fácil:
Agora vamos calcular a probabilidade de cada um desses lucros.
Passo 4
Pra calcular a probabilidade do cara lucrar 200 reais, é só a gente calcular a probabilidade de saírem 3 laranjas.
Em cada disco a gente tem um total de 14 possibilidades (14 imagens), sendo 2 delas laranjas. Então a probabilidade de sair uma laranja em um dos discos é:
Mas a gente quer , 3 laranjas nos 3 discos, que será:
Passo 5
Pra calcular a probabilidade do cara lucrar 150 reais, é só a gente calcular a probabilidade de saírem 3 Bananas.
Em cada disco a gente tem um total de 14 possibilidades (14 imagens), sendo 3 delas bananas. Então a probabilidade de sair uma banana em um dos discos é:
Mas a gente quer , 3 laranjas nos 3 discos, que será:
Passo 6
Fazendo o mesmo racicínio para as maçãs e os morangos a gente tem que:
A probabilidade de se lucrar 100 reais, que é a probabilidade de sair 3 maçãs é:
E a probabilidade de lucrar 50 reais será:
Passo 7
Falta só calcular a probabilidade de qualquer outro resultado sair, fazendo o cara ter prejuízo de 50 reais.
Pensa comigo!
Concorda ?
Logo:
Passo 8
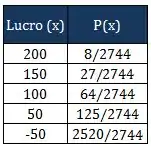
Vou montar uma tabelinha agora com os possíveis lucros que o jogador pode ter e a probabilidade de cada um acontecer, tranquilo?
Passo 9
Chamando de a v.a. que representa o lucro de um jogador em uma jogada.
Pra gente saber o lucro médio pra uma jogada, a gente tem que calcular a esperança dessa variável.
Como se trata de uma variável discreta (que assume valores específicos: 200, 150, 100, 50 e -50), a esperança é dada por:
Usando a nossa tabela...
Passo 10
Agora pra saber o lucro esperado de 10 jogadas, a gente precisa calcular:
Concorda ?
Usando as propriedades da esperança a gente tem que:
Que a gente já calculou.