UFRJ – Física 2 – 2019.1 – 2CH – Discursiva
. O ciclo de Brayton é uma representação dos processos térmicos que ocorrem nas turbinas a gás, como as usadas na aviação. Suponhamos que se trata de moles de um gás ideal com . O ciclo se divide em etapas, incluindo uma compressão e uma expansão adiabáticas reversíveis, como mostra a figura abaixo:
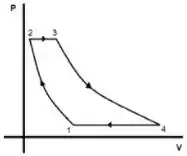
Calcule a variação da entropia em cada etapa do ciclo.
Passo 1
Vem comigo que a gente derrota essa questão!
O enunciado pede a variação da entropia em cada etapa do processo. A variação de entropia é dada por:
Nessa máquina temos dois processos adiabáticos e , onde .
E dois processos a pressão constante e , onde
Vamos avaliar então.
Passo 2
Nas etapas adiabáticas como temos que , temos:
Logo , então .
Passo 3
Nas etapas com pressão constante, temos:
Integrando os dois lados temos:
Então temos que:
Prontinho, temos tudo o que ele queria!