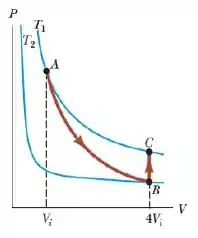
Suponha que n mols do gás ideal da figura abaixo se expanda até quatro vezes seu volume inicial. Como se vê, as temperaturas inicial e final são as mesmas. Calcule a variação da entropia ΔS do gás.
a) ΔS = nRln2;
b) ΔS = nR;
c) ΔS = nR/ln2;
d) ΔS = nR/ln4;
e) ΔS = nRln4;
Passo 1
Vamos lembrar que a entropia é função de estado! Ela não depende do caminho. Vamos calcular então a entropia no processo AC, por ser uma isoterma e mais fácil de calcular.
Aplicando a 1ᵃ Lei da Termodinâmica:
Mas a temperatura em A é igual à temperatura em C. Então a variação de energia interna vai ser zero!
Show!
Passo 2
Vamos calcular o trabalho em AC:
Passo 3
Lembra que a variação de entropia a gente calcula:
E aqui no caso:
Como entre os pontos A e C a temperatura não varia:
Resposta
Letra E.
Exercícios de Livros Relacionados
Suponha que 1 m o l de um gás monoatômico ideal inicialmente à pressão p 1 e ocupando um volume V 1 seja submetido sucessivamente a dois processos: ( 1 ) uma expansão isotérmica até um volume 2 V 1 e
Suponha que 0,55 m o l de um gás ideal seja expandido isotérmica e reversivelmente nas quatro situações da tabela abaixo. Qual é a variação da entropia do gás para cada situação?
Quanta energia deve ser transferida na forma de calor para uma expansão isotérmica reversível de um gás ideal a 132 ° C se a entropia do gás aumenta de 46,0J / K ?
Suponha que 4,00m o l s de um gás ideal sofrem uma expansão reversível isotérmica do volume V 1 para o volume V 2 = 2,00 V 1 a uma temperatura T = 400K . Determine (a) o trabalho realizado pelo gás e
Uma caixa de 1,0 L contém N moléculas de um gás ideal, e as posições das moléculas são observadas 100 vezes por segundo. Calcule o temo médio que deve decorrer antes que se possa observar toas as N mo