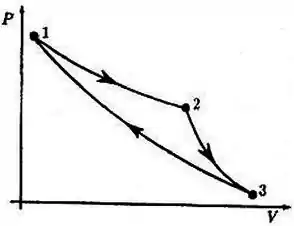
Um engenheiro propôs à sua empresa construir uma máquina térmica onde um gás ideal monoatômico sofre os processos indicados no diagrama da figura:
: processo isotérmico
: processo adiabático
: processo adiabático
A proposta foi rejeitada.
Quais das afirmativas abaixo são justificativas corretas para esta rejeição:
- Esta máquina não funciona pois viola a segunda lei da termodinâmica.
- Esta máquina não interessa pois tem uma eficiência muito baixa.
- O ciclo é inconsistente. Uma das etapas indicadas não pode ocorrer.
- Esta máquina não funciona pois viola a primeira lei da termodinâmica.
- I e III
- I e IV
- I
- IV
- II e IV
Passo 1
Vamos analisar essas afirmativas.
Afirmativa I:
Violar a Segunda Lei da Termodinâmica em um ciclo significa que todo o calor fornecido é convertido em trabalho (sem desperdício de calor pra fonte fria). Nós sabemos que na prática isso é impossível, não é mesmo?
Ou seja:
Violar a segunda lei significa que .
Vamos investigar isso.
Passo 2
Vamos aplicar a Primeira Lei em cada processo:
Processo -:
Como esse processo é isotérmico, então .
Logo:
Processo -:
Como esse processo é adiabático, então .
Logo:
Processo -:
Como esse processo também é adiabático, chegamos ao mesmo resultado:
Passo 3
Agora podemos calcular o calor que entra e o trabalho realizado no ciclo.
Calor que entra:
Trabalho do ciclo:
O trabalho é calculado da seguinte forma:
pois o processo é isotérmico.
Os trabalhos e são calculados dessa forma:
Como o gás é monoatômico, .
Somando essas duas parcelas:
Como (processo isotérmico):
Logo:
Além disso, vimos que
Então .
Substituindo na Primeira Lei do ciclo:
Isso viola a segunda lei da termodinâmica.
Pois, nesse caso, teríamos um rendimento igual a:
E isso não está de acordo com a segunda lei!
Outra forma de pensar é que a variação de entropia desse ciclo é nula (por que a entropia é uma função de estado)
Como só há troca de calor na etapa e nessa etapa o gás absorve calor da fonte quente, temos que a variação de entropia das fontes só ocorre nesse processo. Como
Então nesse processo a fonte quente tem a sua entropia diminuída, ou seja, no ciclo a variação de entropia é negativa
A variação de entropia do universo é dada por
Como um desses caras é negativo e o outro é nulo temos que
O que viola (de novo) a segunda lei! o/
Afirmativa I é verdadeira.
Pelas alternativas, eliminamos as letras (d) e (e).
Pelas que sobraram, já podemos ver que a afirmativa II é falsa. Então basta analisar as afirmativas III e IV.
Passo 4
Mas se você quiser, vamos analisar a afirmativa II:
Acabamos de ver que a eficiência dessa máquina é .
Então essa eficiência não é baixa de jeito nenhum!
Afirmativa II falsa, como já sabíamos.
Passo 5
Afirmativa III:
O processo adiabático que estamos considerando é reversível.
Isto é, podemos caminhar sobre a curva adiabática em um sentido ou em outro.
No ciclo, estamos vendo duas curvas diferentes para um mesmo processo adiabático!
A curva -, na verdade, deveria ser igual à curva -, retornando pelo mesmo caminho, já que o processo é reversível.
Se você não acredita, basta lembrar que num processo adiabático a pressão e o volume têm que obedecer
Se você aplicar isso no processo
E se aplicar no processo
Juntando a gente teria
Só que o processo é um processo isotérmico que obedece
Só dá pra obedecer essas duas equações se fosse ! Só que o pra gás monoatômico é , logo esse negócio aí não pode tá certo!!!
Portanto, essa etapa não pode ocorrer!
Afirmativa III correta.
Passo 6
Afirmativa IV:
Perceba que aplicamos a Primeira Lei nos processos e no ciclo como um todo.
Embora esse ciclo tenha violado a Segunda Lei, não teve nenhum problema com a Primeira Lei.
Então, a afirmativa IV é falsa!
Logo, as afirmativas corretas são I e III.
Resposta
Alternativa (a).