O ciclo de Joule, representado na figura abaixo, onde e são adiabáticas, é uma idealização do que ocorre em uma turbina de gás: e representam respectivamente aquecimento e resfriamento à pressão constante; é a taxa de compressão e . Seja o coeficiente adiabático do gás ideal submetido ao ciclo dado por .
Dados: , e
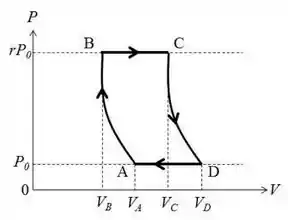
- Calcule o calor trocado no processo () em termos de , , e
- Calcule o calor trocado no processo () em termos de , e
- Usando os resultados do item anterior, calcule o rendimento do ciclo em termos de e
- Sabendo que mols do referido gás são usados na turbina, calcule a variação de entropia no processo em termos de e
Passo 1
O processo é uma expansão isobárica. O calor recebido é dado por
Onde é o calor específico a pressão constante e é dado por
Usando a equação dos gases ideais temos
De forma que
Como pelo enunciado
Assim
Passo 2
O processo é uma contração isobárica. O calor recebido (nesse caso, retirado) é dado por
A variação de temperatura é dada por (usando a equação dos gases ideais)
Como
(o sinal de menos indica que o gás perdeu calor)
Assim
Passo 3
Temos que o rendimento do ciclo é dado por
Passo 4
Essa resposta tá quase perfeita. Precisamos escrever o rendimento em função de e e temos que eliminar esses volumes e .
O processo é uma compressão adiabática. Lembra como a gente relaciona a pressão e volume em um processo adiabático? É assim ó:
Substituindo as pressões de e e isolando a razão
Agora jogando isso no nosso rendimento
Passo 5
Temos que uma variação infinitesimal de entropia é dada por
No processo , já vimos que
Na forma diferencial
Assim
Por outro lado
E como , temos que
E então
Resposta
(a)
(b)
(c)
(d)