A figura abaixo é o diagrama do ciclo de uma máquina que faz uso de de um gás ideal monoatômico. Os processos são adiabáticos, enquanto são processos a pressão constante (isobáricas). Sejamas temperaturas nos estados , respectivamente. Para as questões abaixo, expresse seu resultado em termos das temperaturas, da constante dos gases, , e do número de moles, .
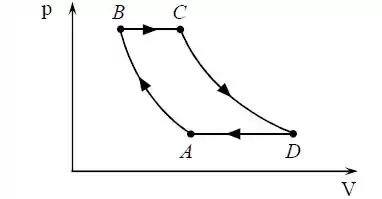
- Calcule o calor trocado em cada etapa do ciclo e o trabalho total realizado no ciclo.
- Calcule a eficiência de uma máquina operando neste ciclo fazendo uso de um gás ideal.
- Calcule a variação da entropia do gás em cada etapa do ciclo.
Passo 1
a)
Para os processos , que são adiabáticos, temos:
Já para o processo , que ocorre à pressão constante, temos:
Assim:
A expressão do calor do processo vai ser parecida, apenas precisamos trocar as temperaturas:
Para um ciclo, temos :
Assim:
Passo 2
b)
A eficiência é dada por:
Qual é o calor absorvido? É o calor que é trocado em . Afinal de contas, ali o gás se expande, o que indica que ele está recebendo calor. Assim:
Assim:
Passo 3
c)
nos processos adiabáticos não ocorre transferência de calor, assim, a variação de entropia é nula. Então:
Já nos outros processos:
Assim:
Resposta
a)
b)
c)