Um gás ideal diatômico descreve o ciclo definido pelas seguintes etapas:
: processo a volume constante , desde a pressão até .
: expansão a pressão constante , do volume até .
: processo a volume constante , de até .
: compressão a pressão constante , de até .
Desenhe o ciclo num gráfico versus , sendo Pa e
Dado que o número de mols do gás é tal que , calcule a temperatura em cada vétice.
Obtenha o trabalho realizado pelo gás em cada ciclo.
Obtenha o calor trocado em cada etapa do ciclo, indicando se é recebido ou cedido pelo gás.
Calcule a eficiência de um motor térmico operando segundo o ciclo .
Calcule a variação de entropia da etapa e a variação de entropia no ciclo completo.
Passo 1
Vamos primeiro montar o gráfico de acordo com as informações dadas no enunciado:
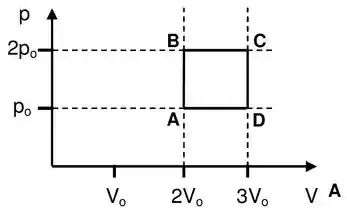
Podemos ver claramente no gráfico as transformações a volume constante e a pressão constante.
Passo 2
Como temos o valor de e de , podemos achar a temperatura em cada vértice utilizando a lei dos gases ideais, lembre-se que
Vamos começar com o vértice :
Substituindo os valores, temos:
Passo 3
Vamos agora para o vértice :
Passo 4
Para o vértice , temos:
Passo 5
Para o vértice , temos:
Passo 6
Quando temos um ciclo, sabemo que o trabalho realizado é igual à área do retângulo , ou seja:
Passo 7
Para determinar o calor trocado em cada etapa, vamos recordar da equação para o calor a volume constante e a pressão constante, que são, respectivamente:
Lembrando que para um gás diatômico, temos:
Dito isso, podemos determinar o cator trocado em cada processo do ciclo!
Passo 8
Vamos começar com os processos a volume constante, vamos calcular primeiro e depois :
Para , temos:
Passo 9
Agora vamos calcular o calor trocado no processo a pressão constante, primeiro e depois :
Para , temos:
Perceba que em todas as contas desse item juntamos , pois já temos esse valor!
O sinal indica se o calor é recebido() ou cedido().
Passo 10
Para uma máquina térmica, temos que a eficiência é dada por:
Onde é o calor recebido pelo gás. Podemos calcular esse calor simplesmente somando os do item anterior!
Substituindo na fórmula da eficiência, temos:
Passo 11
Para calcular a entropia, vamos relembra da fórmula:
Substituindo pela fórmula usada em processos a pressão constante, visto que esse é processo entre e , temos:
Para um ciclo, temos que a entropia é zero:
Resposta
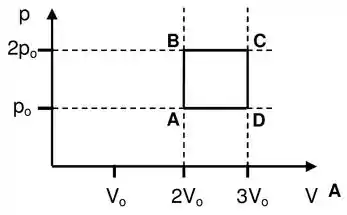
;